Thomas K. Bjorklund has a post at WUWT which tells us a lot about the level of “science” at that blog.
He reveals his theme early:
The discussion below of the first derivative of a temperature anomaly trendline shows the rate of increase of relatively stable and nearly noise-free temperatures peaked in 2006 and has since declined in rate of increase to the present.
There it is — and really, folks, this is all he’s got. He claims that the rate of warming has declined from 2006 to the present. There’s other stuff for window dressing; this is his real argument.
Where does he get that? He takes the global temperature data from HadCRU (the HadCRUT4 data set) and fits a 6th-degree polynomial, then calls that “relatively stable and nearly noise-free temperatures.” Here’s his graph:
Figure 1. The black curve is the HadCRUT4 time series of the mean monthly global land and sea surface temperature anomalies, 1850-present). Anomalies are deviations from the 1961-1990 annual mean temperatures in degrees Celsius. The red curve is the trendline of the HadCRUT4 data set, an Excel sixth-degree polynomial best fit of the temperature anomalies. The green curve is the first derivative of the trendline converted from units of degrees C per month to degrees C per decade, that is; the slope of the trendline curve.
I prefer my own version; I’ve plotted the 6th-degree polynomial as a blue line, and I’ve added light blue shading around it to indicate the uncertainty range (95% confidence interval):
Now to the heart of the matter: here’s his graph of the rate of warming according to the 6th-degree-polynomial model, as a green line:
He’s also added CO2 emissions data in blue, but that doesn’t matter. His graph sure makes it hard to see how the rate itself has changed. Here’s a better version; I’ve plotted the rate according to the 6th-degree-polynomial model as a blue (rather than green) line, and again I’ve added light blue shading to indicate the uncertainty range (95% confidence interval). And since he mentioned the HadCRUT4 data go back to 1850, I’ll show all of it:
Look at the uncertainty range before the year 1870 and after the year 2000. According to the 6th-degree polynomial model, the warming rate right now might be as high as 0.044 °C/yr — that’s 4.4 °C/century. Do we really have evidence that the warming rate declined since 2006?
Of course not. The uncertainty range explodes near the ends of the time span. As I’ve mentioned in the past, this is one of the characteristic drawbacks of using high-order polynomials to approximate a long term trend. Far from the endpoints they do a great job, but their endpoint behavior is a disaster. The higher the order, the worse the disaster. Especially when estimating rates, not just values.
Are there better ways? Lots.
Readers know I’m partial to the lowess smooth (no disrespect to fans of spline fits, singular spectrum analysis, Bayesian smoothing, etc.). For the trend itself it approximates this (red line with pink shading for the 95% confidence interval):
Now to the heart of the matter: here’s the rate of warming according to both the lowess-smooth model (in red) and the 6th-degree polynomial model (in blue):
Is there any actual evidence that the rate of warming has declined since 2006? No.
Bjorklund also mentions the data from NASA; does it show evidence the rate of warming has declined since 2006? No.
The uncertainty range gets wider near the endpoints, in both models; that’s just unavoidable. But the graphs show how the endpoint problem is so much worse for the high-order polynomial (6th-degree) fit than for the lowess smooth.
If you’re interested in how the rate of global warming may have changed recently, I’ve posted about that myself. As for Bjorklund, his claim has no evidence at all, just the mixture of a bad choice of smoothing method and ignorance of the uncertainties involved.
This blog is made possible by readers like you; join others by donating at My Wee Dragon.
Open Mind 
“Give me four parameters, and I will fit an elephant; five, and I will make him wiggle his trunk.”–John von Neumann
I’m sorry, but Bjorklund’s post is an utter embarrassment. It demonstrates not just a surprising ignorance of statistics, data analysis…, but a profound misunderstanding of the purpose of curve fitting. Really, once you’ve published anything this fricking stupid, you should just retire from public life and hope your own children forget you ever existed!
Yeah, usually there’s special treatment of data points at ends of series for exactly the reasons @Tamino cites. The net effect is that they are uncertain. This can also occur if points along a series are missing: By rights, the uncertainty envelope should momentarily balloon.
Some people use tricks, like reflection … meaning that that in order to complete the fit, if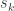
indicates the 
-th point of a series and 
is the number of points, hypothetical additional points 
are introduced where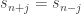 
for small 
. This technically works, but the resulting estimated uncertainty is understated, and so I don’t like it.
For an interesting discussion and application, Muggeo (2014) explores some of these issues in the modTempEff package of R for studying “epidemiological time series of mortality, temperature, and other confounders”. Also the 2010 paper by Eilers and Marx describes the placement and role of knots when using penalized- and B-splines. It includes some beautiful illustrations of how these work.
Did anyone point out that – at WUWT – global warming was supposed to have stopped altogether in 1998?
The various nonsense versions of the AGW ‘hiatus’ were mainly driven by the strong 1998 El Niño and the appearance of the strong La Niña years either side of the 2010 El Niño. This Wattsupian claim that AGW has been slowing down since 2006 is presumably picking up on the depressed global temperature during those La Niña years (and somehow managing to not pick up on the rather dramatic post- 2014 increase in temperature.
Prompted by your question, I did take a squint at some of the demented babble being posted about the piece of mind-numbing Wattsupian nonsense discussed here. Most of it digresses into rants about it being very cold for November, whether it’s the Sun wot dun it, if the CO2 rise is anthropogenic, then a lot of stuff about the Figure 2 in the Wattsupian OP (the third graph in Tamino’s OP above) which shows the atmospheric CO2 concentration in 1900 down at 30ppm (no typo – thirty ppm). The graph appears to be plotting some measure of emissions not atmospheric concentration, but using some scaling scheme that is crazy even by Wattsupian standards.
Funny you would mention that… Some nitwit on twitter just cited this paper as evidence that there had been no significant warming over the last 170 years (that was the headline at WUWT), despite the fact that it addresses 2031 projections and not historical warming.
THEN, he said that there had been no warming over the last 20 years. For some reason he got sorta quiet when I pointed out to him that the “paper” he had just cited showed a distinctly positive trend over the past 20 years.
Ah, *this* Tom Bjorklund:
https://www.uh.edu/nsm/earth-atmospheric/people/faculty/tom-bjorklund/
Interesting person. As his biography notes “His current studies have focused on the geological evolution of the Los Angeles basin and continental borderland and its impact on the petroleum potential of the region and the application of advanced seismic attributes to characterize complex reservoirs. He has supervisory and technical experience with three major oil and gas companies that range from exploitation and close-in exploration in the West Coast, Rocky Mountain, and Mid-continent areas of the US to international operations in the offshore of Trinidad and China and in the Northwest Territories of Pakistan.”
Why am I not surprised?
What happens if you use a 5th-degree or 7th-degree polynomial?
@Keith McClary,
Waste of time to try 5th or 7th. There’s a general theory for this and a known way to proceed. First you need a uniform criterion, like mean squared error, which should be minimized. Next, the model should be penalized by the number of parameters it uses: The more the number of parameters, the less attractive the model is, per the discussion regarding the Akaike criterion, for example. Finally, the fit should be done with some impartial mechanism which takes into consideration out-of-sample fits, correcting for overfitting like cross validation (see also generalized cross-validation).
You throw all these ingredients together, and y’end up with a requirement for local regression, of which splines of various flavors and lowess, which is what @Tamino and many others are fond of using as a default.
bad science
Not even bad science. Not science.
Keith, Climateball players making ersistant use of polynomials of higher degree than three may end up in a corresponding circle of Dante’s Inferno.
Perpetrators of sixth order statistical violence against thermodynamics or commonsense may land on the far side of the Styx in the blood-boiling river Phlegethon.
And looking at the beginning of 6 degree polynomial fit warming rate would indicate that warming was most intense in the 80’s of 19th century.
As I posted elsewhere, this one excerpt tells you all you need to know about the author’s expertise:
Russell:
I’m just wondering if he tried 5 and 7 but the resulting “warming curve” didn’t do what he wanted it to.
A 6th degree polynomial? Had his crayons all melted? WTF is that noise.
“Had his crayons all melted?”
Perhaps if they had, he wouldn’t be in denial about warming?
So where was this “article” published?
The publication at WUWT manifestly was intended as kinda open review :-)
Hi Tamino,
I know that this is not on topic and it may not be of interest to you, but i was wondering if you knew whether or not climate change was making 5 to 7 day weather forecasting less accurate. Over the last couple of years, I feel that I have noticed this from the Bureau of Meteorology for Canberra (Australia), but I do not have the recorded data from previous years and I know that trusting my memory is not a wise thing to do.
David
I don’t have the data either, but forecast skill has been steadily improving so rapidly that, even if climate change had a negative effect on forecasts, it could only slow the rate of improvement. Forecast skill does vary from year to year because some weather patterns have higher predictability than others.
Does “forecast skill has been steadily improving so rapidly” apply to ENSO?
Tamino,
When you run the Lowess smooth, what number of years do you use as a cutoff and how do you determine that? It looks like your using about 30 years.
Out of interest, what would his predictions have been if he’d used this approach in past years? Say 2000, or 2005, or 2010.
about forecasting ENSO–here is the latest I’ve found:
https://www.climate.gov/news-features/blogs/enso/enso-forecast-mash-ups-what%E2%80%99s-best-way-combine-human-expertise-models
There is not much skill at more than a year out.