In the past I’ve explored simple energy balance models for the evolution of global average temperature. One of the important things to note is that a “1-box” energy balance model — in which the entire climate system is considered to have a single time constant — isn’t really sufficient. It can give a pretty good fit, but for a more realistic estimate you need at least two boxes. One represents rapid response to climate forcing — think of it as the “atmosphere” if you wish. The other is for slower response — think of it as “ocean” if you wish, or as “upper ocean,” or as “everything else.” One could be even more realistic with more than two boxes, after all the deep ocean certainly effects climate but with a longer time scale still, and there’s the cryosphere on top of it all, but rather than go the way of the full-blown computer simulation model, let’s see what happens if we just use a 2-box model with two time constants. We’ll think of box 1 as the atmosphere, so that it should correspond to the surface temperature we’re all familiar with.
Given climate forcing as a function of time, one can integrate the 2-box model equations of motion numerically. But this isn’t really necessary because the equations can be solved in closed form. The solution is a superposition of the forcing function exponentially smoothed with both time constants. Temperature for box 1 will be
,
where is the forcing function exponentially smoothed with the first time constant,
with the second time constant,
and
are the expansion coefficients (which are related to the heat capacity of the boxes, the time constants, and climate sensitivity), and
is an integration constant.
One can try to estimate relevant physical quantities (heat capacities, rate of heat exchange between the two boxes, and time constants) from basic physical considerations. This is quite difficult, and always seems to lead to disagreement. But if we’re mainly interested in surface temperature then we don’t have to do this. We can determine the expansion coefficients and the time constants empirically, by fitting the exponentially smoothed forcing function to observed temperature data. This doesn’t enable us to divine the heat capacities or heat exchange rate, but it will show whether or not the assumed forcing function can lead to the observed temperature change and it will enable us to estimate climate sensitivity — an important parameter. That will be equal to the sum of the expansion coefficients in deg.C/(W/m^2), and if we multiply it by 3.71 we’ll get the climate sensitivity to doubling CO2.
The last time I did this I used climate forcing data from NASA which only went through 2003. Since then NASA have updated their forcing data through 2011. Let’s repeat the experiment and see what happens.
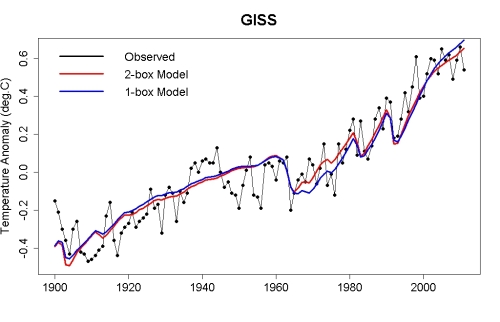
The forcing data are at annual time resolution, so I’ll use annual average temperature from NASA GISS. Computing the 2-box model gives this:
The fit is pretty good, except that there are rapid fluctuations (noise if you will) that are not accounted for. If instead we use a 1-box model, the fit is still good but decidedly not as good as the 2-box model:
One of the things left out of the 2-box model is the influence of the el Nino southern oscillation (ENSO). This is not a climate forcing; it doesn’t represent a change to the energy budget of the climate system as a whole. Perhaps the best way to treat it would be to introduce a time-variable heat exchange rate between the two boxes. What I’ll do instead is simply treat it as a temperature perturbation. I experimented with treating it as a forcing, or treating its time derivative as a forcing, but the results don’t indicate that either of those approaches has any advantage.
I characterized ENSO by the southern oscillation index, or SOI. Bear in mind that unlike indexes like MEI (multivariate el Nino index), the SOI is negative during el Nino conditions and positive during la Nina conditions, so we expect the sign of its effect to be reversed relative to those other indexes. We also know that ENSO has a delayed effect, lagging by about 6 months, so I computed the average SOI from each July through the following June to represent the annual impact of ENSO. Then I fit a model consisting of exponentially smoothed forcings and the lagged SOI. That gave this model, which frankly, strikes me as not just good, but stunningly so:
The best time constants turned out to be 2 years and 26 years. This is in good agreement with the results of GISS climate simulation models, which suggest about a 30-year time scale for the climate system as a whole. The “fast” coefficient was 0.17 deg.C/(W/m^2) and the “slow” coefficient 0.51 deg.C/(W/m^2), indicating overall climate sensitivity of 0.68 deg.C/(W/m^2), which gives a sensitivity to doubling CO2 of just about 2.5 deg.C.
It also shows that present estimates of climate forcing, combined with a sensible physical model, reproduce observed temperature.
That temperature hasn’t risen as rapidly over the last decade or so as in the preceding decades is in large part due to el Nino. As shown here, the influence of el Nino over the last decade has been decidedly cooling. But that isn’t part of the signal, it’s part of the noise — noise of a physical origin, but not persistent temperature change. If we use the 2-box model to estimate the influence of ENSO, we see its recent cooling influence plainly:
If we take the full 2-box + ENSO model and remove the influence of ENSO, we see what the model suggests as temperature change apart from this fluctuation:
And ENSO isn’t the only impermanent flucutation contributing to less recent warming. Solar forcing has been less than in the preceding decades too. Perhaps I’ll compute and remove the influence of solar variations and volcanism, in order to isolate the anthropogenic influence further.
The salient point is that those who are trying to “explain” temperature change over the last decade are barking up the wrong tree. There’s nothing to explain. Temperature has continued to evolve according to climate forcing and known noise factors like ENSO. There is certainly no need to invoke a mysterious influence of the Atlantic multidecadal oscillation or some mythical 60-year cycle. There’s nothing to explain.
Sooner rather than later we’ll see more surface-warming influence of el Nino. The sun will continue to vary, but within the narrow range it has varied in the past. The long-term evolution of global temperature will be dominated — yes, dominated — by the forcings that are changing by large amounts and will continue to do so over the next century. Primarily, that’s greenhouse gases. No fantasy ocean oscillation or mystery cycle will save us from what is coming. It’s already hot in here, and it’s gonna get a helluva lot hotter.







The “influence of ENSO” chart looks a bit like an upside down hockey stick … How long before someone tries to extrapolate that to forecast future climate? Perhaps with a 60 year cycle thrown in for good measure.
Thank you once again Tamino. It’s amazing to see how closely even very simple models match the real world.
Speaking of fantasy AMO claims, I just debunked Tung and Zhou 2013 so others don’t have to.
This is wonderful – such results from such a simple model! (btw, am loving your new book. If it had more about effect sizes, and other disciplines to avoid the “gotchas” of the p-value significance ritual, it would greatly shrink the number of “go-to” books as I fumble through statistics for work – some materials on economic significance and causality and robustness of p-value would be a treat. The sections on non-parametric statistics and robust statistics – fantastic! Very happy I purchased your book on the first day of it being offered.)
[Response: Thank you very much. It was hard to decide what to include and what to leave out, and I’ve second-guessed my own choices quite a bit. For instance, I wrote a chapter on the Poisson distribution but decided to omit it — because I wanted to focus on “just the basics.” With time, I’ll have a better idea of what to change.]
Now that is impressive. It also implies the NASA forcing data is pretty good.
What Dumb Scientist wrote in his first paragraph.
I love this post.
I think it will be “game over” when we get the next big El Nino. At that stage the “skeptics” will shut up, and we can somewhat belatedly start fixing the problem.
[Response: I hope your optimistic expectation comes to pass.]
Not a chance. Going on past behaviour, the fake skeptics will treat the next big El Nino as just another 1998. About three years after that, when temperatures go down even slightly (but this decade is still hotter than all preceding it), then we’re headed for another freakin’ ICE AGE!!!1!!! The Escalator; it never stops giving.
BTW, that 26-year delayed 2nd box response that tamino found – that’s the kicker. The BAU wingnuts can’t deal with anything that doesn’t give them immediate gratification in the next quarter, let alone for 26 years. We’re doomed.
I’ll also be purchasing tamino’s book shortly. Badly in need of some stats chops :-\
After the next El Niño we won’t need three years to get a solid carbon tax in place. Last weekend I joined 40,000 people in bitter cold to ask for a carbon tax and to deny the XL Pipeline (see Joe Romm’s opinion of what hilarity will ensue when John Kerry’s influence as the nation’s foremost climate hawk and Secretary of State is felt). In September of 2011 there were hundreds of us. Six months later there were ten thousand of us. 22 months later there were forty thousand of us.
So what if media ignored it completely. That doesn’t discourage the forty thousand that crossed the nation to freeze our asses off for four hours. It won’t discourage us when next year we are 80,000. Or the year after when we are 200,000. And when it’s 300,000 and the El Niño year hits, the corner will be turned. 2015. Let’s hope that’s early enough.
Thanks Tamino for some reality check… Ernst K asked “How long…” so I’ll throw in the mythical 60 year cycle by eyeballing here and say that the 2040s should be hotter globally than never before 2013, if the sun won’t do something it hasn’t done never before.. :-P.
Just a quick question. How do NASA determine the forcings?
This is, I assume, from GISS. The total forcing is a sum of several components such as tri-atomic atmospheric gases (by species), solar variations and aerosols (primarily from large volcano eruptions; note the down spikes in the summary forcing).
I don’t want to seem like a fake skeptic, but I need to ask this. Are the forcings in any way based on the existing temperature record?
That is, could the good agreement of the two box model driven by forcings be a particularly good match because the forcings were based on the temperatures record?
[Response: As far as I know (based on comments from Gavin Schmidt at RealCliamte): No, not at all.
Fake skepticism is bad. Real skepticism is good.]
John Brookes said: “I think it will be “game over” when we get the next big El Nino. At that stage the “skeptics” will shut up, and we can somewhat belatedly start fixing the problem.”
More likely they will lay low for a year or two and then start pointing out how there’s been no warming since 201x.
If the denailists arguments were based–hell, if they were even cognizant of–empirical evidence, I might agree. If the collective learning curve of the denialists had a positive slope, I might agree. However, this isn’t about empirical evidence or learning. Willard “Micro” Watts and the other main denialists have too much invested in continuing the denial. They will start out be saying what “HUUUUGGGGEEEE!!!!” El Nino it is, and then we’ll be back to the “no warming since…” arguments. And of course the lukewarmers lament that it’s too late to do anything now and it’s the fault of the alarmist scientists.
The denialists collectively will keep mining right down that vein of stupidity until they reach the motherlode.
Indeed…You can see how they’ll handle it in terms of things that are at the moment happening faster than most everyone was predicting, like disappearance of summer arctic sea ice. This has nothing to do with evidence.
What I think might happen is a drop-off in interest in Watts’ site, but the hard-core denialists will go along doing what they do best.
Astoundingly clear – the ENSO plus 2-box model is indeed stunning in its accuracy. Thank you for the clarity.
(And yes, I’ve ordered your stats book, and may even finish reading it sooner or later…)
still eyeballing I’ll throw a guess for the next largish el Nino for late 2015 since they (eyeballing) seem to be occurring both sides of the solar maximum. I haven’t done any calculations on this though, but on la nina there is
http://journals.ametsoc.org/doi/abs/10.1175/JAS-D-12-0101.1?journalCode=atsc
yes there are a couple of massive outliers (c,1970 and c,1908) wrt the previous comment in the post-1900 record, in case someone actually believed that.
One thing I’ve wondered is whether the forcings from greenhouse gases can perturb ENSO- for example making La Ninas more frequent and El Ninos less frequent or vice versa. I’ve done a little poking around on this, there’s nothing I could see in Pierrehumberts book on this, but there are a few references that I could find in the literature that appear to discuss the topic
for example
DOI: 10.1029/2007GL030854
but I’m not seeing a physics based idea of warming altering ENSO and I’m not sure I’m asking google scholar the right questions. I’d appreciate any pointers to good discussions of this.
Almost surely yes. A paper to contemplate is
Variability of El Niño/Southern Oscillation activity at millennial timescales during the Holocene epoch
http://www.nature.com/nature/journal/v420/n6912/full/nature01194.html
paying especial attention to the earliest times.
By the way, I doubt the claim of an actual about 2000 year quasi-period despite the authors’ claim of ‘statistical significance’.
One can try to estimate relevant physical quantities (heat capacities, rate of heat exchange between the two boxes, and time constants) from basic physical considerations. This is quite difficult, and always seems to lead to disagreement.
———-
Lucia banged on about this. Can’t remember if there was a resolution.
However I would like to introduce a distinction between various kinds of 2 box models, just in case it helps some people. That is the black box kind and the white box kind.
In a black box model the input/output response is analysed and a mathematical description derived. in electronics engineering terms, an equivalent circuit. The equivalent circuit is not necessarily the same as the actual circuit inside the black box. That actual circuit is hidden from view.
In a white box model you can see inside the box and see such things as water, air, ice and land and know what their physical properties are and the boundaries between them. Then you can apply some physics to infer the input/output response of the system.
These box models differ as the direction of inference is opposite.
Does that tighten up the concepts a bit?
Resolution does not seem to be her forte.
Some (not Horatio, of course) might claim he forte is just the opposite. :)
That certain two box model combinations with very specific makeups (eg, “atmosphere alone”[with no surface ocean] and “entire ocean”) and very specific time constants are “unphysical” (violate the 2nd law of thermodynamics”) does that mean all are (do)
Lucia took issue with (made great hay of) Tamino’s “surface box” (short) time constant (previously given as 1 year), but Horatio does not recall that Tamino actually specified precisely what his two boxes comprised — eg, whether his ‘surface box” was “just atmosphere” or perhaps “atmosphere plus near-surface ocean water (down to some depth)”.
In the paper by Stephan Schwartz in which he proposed a (what was shown to be a flawed) one box model, Schwartz related a finding by Boer et al that a time constant of about 8 months applies for a “box” that includes the surface ocean down to about 50m.
Include a little more near-surface ocean in the “surface box” and one would have a quite physical “box” with a time constant of 1-2 years.
Good one ! Getting all relevant inputs to make the past of a model reflect observations, is the holy grail of any prediction.
On that, I have a burning question.
In the good old simple hockey stick days, ice cores showed a sequence of glacial periods possibly driven by Milankovitch cycles. Is this data still input in the current models and if so, what would the state of the climate be today, if humans were not affecting it ?
Cause if there was a gradual dip, one could ask: Does humanity need to learn how to globalwarm (new verb) properly, so that we can stay warm during the next glacial ? (joke) Might be a good idea to hold on to some of these dirty old power stations.
The time scales are really different: I think enough so that there would be little or no point including insolation data because they basically wouldn’t change during runs of realistic length. (Perhaps someone will correct me if I’m wrong on that score.)
But there has been some work on the probable effects of anthropogenic CO2 on the glacial cycle; I recall one paper found that we may well have emitted enough already to cancel the next glaciation altogether.
Searching Google Scholar with the terms “anthropgenic co2 next glacial cycle” found over 15,000 results. The top hit was this:
Click to access archer.2005.trigger.pdf
Yes, that’s David Archer of U. Chicago and Real Climate, and whose “Long Thaw” I wrote about here:
http://doc-snow.hubpages.com/hub/The-Long-Thaw-A-Review
‘Money quote:’
“We predict that a carbon release from fossil fuels or methane hydrate deposits of 5000 Gton C could prevent glaciation for the next 500,000 years, until after not one but two 400 kyr cycle eccentricity minima. The duration and intensity of the projected interglacial period are longer than have been seen in the last 2.6 million years.”
Thank you very much for your response. Also very impressed with your concise summary of Archer’s book.
I first asked the question in about 2006. I remember being ‘disappointed’ when even Wikipedia stated that we happen to be experiencing an extended interglacial. In 2007, I had seen enough and left the big city to concentrate on survival. In 2009, I was too busy with that and missed “The Long Thaw”. Still very busy today building that arc, still a long way to go, meanwhile my world is starting to crumble (AUS East coast) and the political climate has not moved.
Our current focus is industrial pollution and it drives most of the models. More recently, we have added land clearing, farting animals and urban heat. Apparently, the initiation of ice sheets only requires a relatively small forcing. It may be worth while to focus on the latter smaller inputs and attempt to prove that the actions of our forefathers have already extended the current interglacial. Archer&Ganopolsky have that as ‘natural evolution’ in figure 3, but it is unlikely that something as physical as Milankovitch cycles has such a large fluctuation.
Again, thank you. It’s time to go and assess the damage.
You might look at Tzedakis et al. (2012) as well: http://www.nature.com/ngeo/journal/vaop/ncurrent/full/ngeo1358.html — “Determining the natural length of the current interglacial.” Bottom line: glacial inception unlikely with CO2 above 280ppm.
My understanding of Milankovitch cycles is that they are driven mainly by changes in northern hemispere summer insolation, which act directly on the ice and snow cover, determining whether ice sheets gradually grow or shrink over thousands of years. That insolation has been declining since the Holocene Thermal Maximum around 8,000 years ago but the decline has been levelling off –
I think that’s why there used to be some debate about whether or not the insolation would decline enough to trigger another glacial maximum in the next few thousand years, but that’s academic now, as the anthropogenic forcing is much larger and faster than the orbital forcing.
To answer your question: Even if we stopped producing CO2 tomorrow, it would take many thousands of years for biological and geological processes to sequester enough carbon from the climate system to get back to a point where declining northern hemisphere summer insolation could be enough to grow large ice sheets again.
Happy to be corrected if any of this is wrong, of course…
Cool graph… what’s the source, if you don’t mind saying?
I think the graph was from one of Hansen’s papers… but I’m not 100% sure. I feel bad that I didn’t put some attribution on it at the time :-(
Tamino, your model without SOI shows an increase of 0.3 °C in the 1900-1930 interval, which would correspond to an increase of the forcing of 0.4 W/m^2, when GISS data show no increase at all.
(http://web.archive.org/web/20100204012840im_/https://tamino.files.wordpress.com/2009/08/netforce.jpg?w=500&h=325)
How is it possible ?
Your 2009 model showed a much lower increase in this period. Where does the difference come from ?
[Response: You are mistaken on all points.
The claim that in the 1900-1930 interval GISS forcing “shows no increase at all” is ludicrous. Take the 1900-1930 forcing data, fit a straight line by linear regression, it indicates a net trend increase over that time span of 0.66 W/m^2.
And because of the exponential smoothing, the impact of the volcanic eruptions of the 1880-1900 period persists long enough to affect the 1910-1930 temperature. The 1880-1900 forcing data are included in the exponential smoothing in order for climate forcing to “spin up” to match reality.
And no, the 2009 model does not show “much lower” increase in this period.]
Very interesting one – but the real challenge would be if you could also fit for the ‘ocean box’ the (instrumental) ocean heat anomaly data from Levitus?
[Response: Those data go deep enough that I suspect an even longer time constant would have to be introduced (so we’d need a 3-box model), especially since that part of the ocean (down to 700m?) is sure to interact significantly with the even deeper ocean.]
1- KevinC has you beat :)
2- What happens if you use different forcing histories? Different groups have different estimations of the forcings, especially for aerosols.
Tamino: There are some very interesting results you can get with this model. I think our code must be pretty similar, but I’ll just ask the questions in case I’ve got the answers wrong:
1. If you apply the resulting model to the RCP scenarious, what do the results look like?
[Response: I don’t have the RCP scenarios.]
2. Using this method you can calculate an exogenous-removed temperature series, by subtracting out the ENSO term *and* the temperature response to the solar+volcano forcings. How do the recent trends on the underlying temperature series compare to the F&R2011 results?
[Response: Haven’t run the numbers yet.]
(The answer to these two questions, when combined, was a bit of an eye opener to me. On the other hand if you compare the step function response of the two box model to Hansen & Sato 2011 then a possible explanation emerges.)
[Response: Are you referring to what is reported on Troy’s blog? I think there are some serious problems with that. Also, what “step function response” are you talking about?]
RCP scenario data is here:
http://www.pik-potsdam.de/~mmalte/rcps/
OK, I’ll tell you what I get. The RCP response to 2010 looks very much like the CMIP-5 results at 2100, although there are slight differences in how you get there. The 2-box model seems to respond a bit more gradually than most climate models.
However the trends I see are a bit lower on recent decades than your F&R results – I don’t have the figures to hand, but IIRC they’re in the range 0.12-0.14. The startling thing to me was that a significantly lower trend than your 0.16-0.17 is still consistent with the CMIP-5 long term projections, although the difference is consistent with the response of the 2-box model being a bit slow.
(No, this isn’t related to Troy’s analysis of F&R.)
OK, I removed the solar and volcanic forcings to isolate the anthropogenic forcing. Then I compute the temperature evolution according to the full model, using only the anthropogenic forcing — no solar, volcanic, or ENSO. The result gives a warming rate from 1979 through 2011 of 0.0155 deg.C/yr. This is a bit lower than, but well within the likely range of, the rate estimated for GISS in F&R 2011.
FWIW, Troy has put up a part III to his discussion.
More questions-have you determined a minimum data set to fit the two box model to see how well you can hindcast or forecast from it? And oh, another question- is there any hope of someone coming up with a good predictive ENSO model? And would it have any value to take the historic ENSO cycle period frequency distributions and create a Monte Carlo forecast to create a 20-40 year ensemble forecast from now?
ENSO model? Only a statistical one is possible; consider AR(2).
As for a 2 box forecast I doubt one can do much better than linear extrapolation for maybe 20 years.
ENSO behavior may be simulated with harmonic oscillator model, but this only (I guess) works on stable climates. If the model could be modified by some empirical variable giving the real history of ENSO one might guess some of the behavior, but since the Earth is going towards temperatures not found during the ENSO record, I don’t know how useful it would be. http://www.knmi.nl/publications/fulltexts/simplerev.pdf
The 2-box + SOI model fit is, in some ways, too good. If you look at the uncertainty estimates in HadCRUT4 due to spatial sampling issues then they are a lot bigger than the discrepancies between your model and the GISS numbers.
I wouldn’t expect a perfect model to match so well.
The other important point I note is that it suggests that the forcing estimates for aerosols in the NASA dataset are pretty good. I wonder if it is possible to vary those forcing estimates to see whether the global temperature record is a good constraint on the aerosol forcing.
My recollection of recent papers on this – eg by Jonathan Gregory – is that the estimate of climate sensitivity is highly dependent on the estimate of aerosol forcing, and that the aerosol forcing is uncertain. So there is not enough observational data to constrain the size of the aerosol forcing, and this means there is not a strong constraint on the climate sensitivity – you can get a higher climate sensitivity provided the aerosol forcing is strong enough to offset the extra warming you would expect as a result.
GISS aerosol forcing runs a bit high, which would explain the comparably high TCR estimate which the two-box models represents. However, the temporal evolution of the aerosol forcing seems indeed captured quite well, though latest research suggests that part of it is stratospheric rather than tropospheric aerosol forcing (wrt the last 10 years).
“Take the 1900-1930 forcing data, fit a straight line by linear regression, it indicates a net trend increase over that time span of 0.66 W/m^2.
And because of the exponential smoothing, the impact of the volcanic eruptions of the 1880-1900 period persists long enough to affect the 1910-1930 temperature. The 1880-1900 forcing data are included in the exponential smoothing in order for climate forcing to “spin up” to match reality.”
OK, but the trend is almost entirely due to the recovery of volcanic eruptions of the 1880-1900 period, which overwhelm the anthropogenic component (Krakatoa in 1883 and Mount Tarawera in 1886) . But if you interpret the rise of the 1900-1930 model as the recovery of volcanic eruptions, then you expect the temperature just *before* the eruptions to be of the same order of magnitude than in 1930 : the big volcanic eruptions should have produced a big dip after 1883. But GISS data starting in 1880 do not exhibit this dip (http://data.giss.nasa.gov/gistemp/graphs_v3/Fig.A.gif ) ( (fortunately they start a few years before Krakatoa so you can test your model on the 1880-1900 period). Of course this require to know the forcing some decades before to account for the exponentially decreasing of the past forcing, but in the period 1815-1880 there was no major eruption reported (http://en.wikipedia.org/wiki/List_of_large_volcanic_eruptions ) and few anthropogenic forcing. So you model should predict an almost flat temperature curve, of the same order as in the fourties, followed by a sharp decrease in 1883-1900 period, and then a recovery, if you extend it in the past – which does not fit with the slow recovery from LIA. I think you are mislead by a “starting point effect” of the big eruptions of 1883 -1886, but the period before does not correspond to the influence of these eruptions (which is by the way hardly visible on the reconstructions).
More generally, you are a statistician, so you know that a model must include a calibration period and a verification period to be convincing, since the calibration on the entire period always give a “best fit” (I expect this is explained in your book !) : so what is the calibration and the verification periods in your computation ?
Here’s a prediction. In a few decades when high temperatures are causing real and undeniable problems the blame will fall on scientists for not trying hard enough to convince us that there would be a problem. After all, someone has to take the fall.
“In a few decades when high temperatures are causing real and undeniable problems the blame will fall on scientists for not trying hard enough to convince us that there would be a problem.”
And when that happens–and I know the denialati will try to puff up their chests, and blame ANYONE but themselves– there will be MANY, multiple terabytes of proof we DID try, really hard, that we DID try to sound the alarm, only to be shouted down by the money of the extractive industries, and venal politicians in bed with same. For my part, I will keep shouting from the tops of whatever altitude I can muster.
So right, Harry.
Actually, we don’t need to anticipate the future strategy of the denialati. Mosher and some of the other lukewarmers are already blaming inaction on the “alarmist” scientists and their “shrill” protestations. I am sure Lavoisier thought cooler heads would prevail right up to the point where the blade lopped his off.
I find it highly unsatisfactory that so many prominent deniers are at an advanced age. They’ll likely pull us a milosevich well before the stuff hits the aircon.
Not Mosher, as far as I know. Let’s drink to his continued good health ;-)
Further to the Keystone XL post & conversation (now closed to comment), I see it’s moving a bit further into the mainstream:
“The Respectable Centrist”
— by Horatio Algeranon
“Respectable Centrist”, that is me
Pipeline-hugger instead of Tree-
Defending American society
From dirty hippies, (for a fee)
“Tarry Pipe”
— Horatio Algeranon’s rendition of “Starry Night” (by Don McClean)
Tarry, tarry pipe
Taints our water black and grey,
Leaks out on a future day,
With tars that show their darkness in the soil.
Shadows on the hills,
Soils the trees and the daffodils,
Foils the bees with the oil spills,
In blackness on the snowy linen land.
Now I understand what you tried to say to me,
How you rallied for humanity,
How you tried to make us see.
We would not listen, we did not know how.
Perhaps we’ll listen now.
Tarry, tarry pipe
Flaming towers that brightly blaze,
Swirling clouds and smoggy haze,
Collect in former skies of China blue.
Climate changing too, farmers’ fields of wilted grain,
Weathered faces lined in pain,
Are roiled beneath the pipeline’s tarry sands.
Now I understand what you tried to say to me,
How you rallied for humanity,
How you tried to make us see.
We would not listen, we did not know how.
Perhaps we’ll listen now.
For we did not trust you,
But still your claims were true.
And when no dope was left to hype
Up that tarry, tarry pipe,
It took our life, as poisons often do.
But you could have told us Keystone,
That pipe was never meant for more
Than profits for a few
Tarry, tarry pipe
Praises sung in Congress halls,
Shameless Feds in Capital malls,
With lies that waste the world you can’t forget.
From the shysters that you’ve met,
The oil men in Armani clothes,
The silver tongues of bloody Roves
Have oiled and poisoned all the virgin snow.
Now I think I know what you tried to say to me,
How you rallied for humanity,
How you tried to make us see.
We would not listen, we’re not listening still.
Perhaps we never will…
Another no budget recording by Horatio (of Tarry Pipe)
Off topic here but your comments option appears closed on more appropriate posts.
Following your comments in a previous post on wildfires where you used non parametric (Theil) regression I wondered if it were possible to use this for temperature trends. A quick search in google-scholar indicates Theil-Sen estimators (TS) are used in climate science but I could not spot an obvious paper analysing global temperature. Are you aware of any?
One of the points made in wikipedia about the ‘Theil-Sen estimator’ is that you can obtain a similar sample variance in slope from fewer data points and the slope should also be less affected by outliers.
Using the annual giss data I think you can use about 2/3rds of the points and get similar results to Least squares regression; so a 15 year period (97-2012 incl.) gives a similar slope as LMS over 26 years (86-2012 incl.). I get a slope of 0.17 C/decade. The error is about 0.05 but I suspect my methodology is inappropriate. On a graph I plotted a 16yr rolling median and it is evident that the 16yr TS line is very similar to the 27yr LMS line. Surprisingly I find 9 of the highest rates of warming occurred in the last 10 years.
Could you comment on how appropriate the method is for estimating the rate of surface warming? Could it be a better estimator for rebutting claims of no warming obtained from short time periods?
PS cross posted at SkS. “16 years – Update and Frequently Asked Questions”
[Response: I’m skeptical that you can get an estimate with the same variance using fewer data points, unless the distribution of the errors is strongly non-Gaussian. My studies (not completely rigorous I admit) indicate that noise in temperature data is Gaussian, although it’s clearly strongly autocorrelated. If so, then generalized least squares (GLS) is the “best” method (least variance unbiased estimator). Ordinarly least squares (OLS), when corrected for autocorrelation, is surprisingly close to GLS.
I also don’t know how autocorrelation will affect the uncertainty in a Theil-Sen slope estimate. But I do know that it will.
Just off the top of my head: certainly the Theil-Sen estimator could be used for temperature data, but I don’t think it would have an advantage over least squares.]