I had some further thoughts about the subject of the last post. Here they are.
I’m more convinced that if I have understood the procedure of Hansen et al. correctly, then the “spread” or “dispersion” of the distribution of temperature anomaly (whether re-scaled or not) will depend on the baseline period chosen. More importantly the relative values for different time spans (say, different decades) will also be baseline-dependent.
It seems to me that the variance for a given time span, say some decade, is the sum of two components: the spatial variance (basically, the different averages value between different regions) and the temporal variance, which includes both the trend and the fluctuations. When we talk about variability of the weather (not climate!) we’re trying to isolate those very fluctuations from both the time trend, and from the spatial variations. Hansen’s method, if I read it correctly, doesn’t remove the spatial variations but includes them.
Suppose we have temperature data for n times , for a set of k different regions/stations A = 1,2,…,k, for a total of N=kn data points. The data might be mean temperature for a single month, or for a single season (like the summer), or for the annual average, but we’ll assume there’s no annual cycle in the data. We can arrange the data into a matrix
temperature at time
at station A.
The mean value at station A will be
.
We can then separate the data into the sum of station averages and local fluctuations
,
where the have the property that their station averages are zero
.
Temperature anomaly will be the difference between the temperature and the mean value during the baseline period
at each particular station A.
,
where for convenience we defined the differences between the station averages and the anomaly offsets
(which are the station averages during the baseline period) as
.
Now let’s compute the mean and the variance of the anomalies. The mean will be
,
since the sum of the terms is zero. The mean squared value of the anomalies will be
.
The middle term vanishes, again because the sum of the terms is zero. Hence the mean squared value is
.
Therefore the maximum-likelihood estimate of the variance is
.
The estimated variance of the data is thus the sum of the variance
of the individual-station fluctuations
, and the variance
of the differences between station means and anomaly offsets
.
It’s that last part which makes the variance baseline-dependent. In particular, if the baseline period is the same as the time span we’re averaging over, then all the station averages will equal their corresponding station offsets
, and all the differences
will be zero. This will cause the estimated variance to be minimum. If, on the other hand, the differences
between station means
and station offsets
show large variance because different stations have warmed differently between baseline and observation intervals, then the last term will greatly increase the estimated data variance.
However, if we want to know whether or not the weather (not climate) is getting more variable, then we really want to isolate the individual-station fluctuations . Therefore I submit that in order to estimate the distribution of the temperature anomalies for estimating temperature variability during some time span (perhaps each decade, or a set of 11-year periods like Hansen et al.), then for each time span computed, then baseline for anomaly calculation should be equal to the time span being analyzed.



It seems like the best thing to do would be to measure the difference between the measurement of choice (daily high, presumably, since we’re in the business of talking about black-swan high-temperature events this time of year) and the trend line rather than a flat baseline. Then, calculate the variance of this time series for a sliding time window. Here, you’d have to make a few choices in terms of (1) how the trend line is calculated and (2) time window width, but any compelling result showing changing variance should be robust against different choices.
Lastly, even some statistical proof of significantly increased variance (going beyond just looking at the graphs) doesn’t mean that the increased variance is at high temperatures. If we’re worried about high-temperature events, it makes more sense to look at something like cumulative density plots of daily high temperature probabilities. Plot temperature on the x-axis, the probability that the daily high is above some temperature on the y-axis (so actually one minus the cumulative density), and put vertical lines showing the historical mean +/- one, two, or three sigmas. Either limit the data to July/August or do some sort of seasonal adjustment and the important question should be easy to answer: are extremely hot days more or less likely today than in the past?
Agreed, assuming the climate variation over the period being analysed is small. However over the last decade the Arctic variation has been quite dramatic. To be absolutely thorough, you could run a lowess smooth through each station (or grid cell) and subtract that from the values. That’ll give you a kind of moving anomaly.
Hansen analyzed 10-year time spans, is that correct (judging by graphs on your previous post)?
[Response: They specifically state 11-year time spans.]
I’m not sure that you’ve captured accurately what Hansen et al. did. My understanding is that they studied the empirical distribution of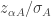 where
where  is the standard deviation of temperature at location A during the baseline period. Now if you model local temperature as trend + noise,
is the standard deviation of temperature at location A during the baseline period. Now if you model local temperature as trend + noise,  . Over a 30-year baseline, the trend can be significant compared to the noise, and $\sigma_A$ varies like the trend vs noise ratio.
. Over a 30-year baseline, the trend can be significant compared to the noise, and $\sigma_A$ varies like the trend vs noise ratio.
I think that the qualitative differences between baseline periods are more related to the effect of than to
than to  . The former period had nearly constant temperatures, thus a
. The former period had nearly constant temperatures, thus a  approximately reflecting actual climate variability. The latter had significant trends, stronger in the areas that warmed most (e.g. the Arctic) which hides some of the warming in those areas and reduces the difference between the 50s and the 00s.
approximately reflecting actual climate variability. The latter had significant trends, stronger in the areas that warmed most (e.g. the Arctic) which hides some of the warming in those areas and reduces the difference between the 50s and the 00s.
The formula that does not parse is: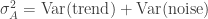 .
.
Sorry about that, the lack of preview is annoying.
For what it’s worth, a few months ago I came to exactly the same conclusion for similar reasons. Therefore, you are correct. [Argumentum ad ipsum]
I filled out an excel spreadsheet demonstrating that constructed data with uniform variance and different trends would seem to produce enhanced variance using Hansen’s technique, and sent it to Hansen’s public email address. I never got a response (it could easily have been filtered away).
My next step was going to be to download all the GISTEMP data and reproduce his analyses with and without local trend estimation, but I’ve never had a chance to do so. All we can say at this point is that his method can’t be trusted for identifying an increase in variance; it would be nice to know whether variance has in fact increased, or not.
Thanks for looking into this.
As the paper was submitted to PNAS on April 5, ( http://www.themoneyparty.org/main/tag/reto-ruedy/ ) and has been in public view for many months now, you could submit a “comment” to the journal.
Slightly unconventional to comment on a paper before its publication, but hey, they asked for it :-)
Tamino, can we expect the seasonal analysis at any time soon. My specific concern is that because winter variability is so much greater than summer variability, it will mask any increase in summer variability if you only examine annual data. On that basis, while you have shown that the analysis in HSR2012 cannot demonstrate their conclusion (or at least any strong interpretation of their conclusion), you have yet to show that there has not been an increase in temporal variance in summer temperature in the US48.
Assume for the moment that variance has not changed over recent decades.
How much would just the observed shift in means affect the probability estimate you made in this post?(1/458,000)
How much more likely would the recent “run of 13” be for your estimate ?
An estimate of such a probability “multiplicative factor” would undoubtedly mean more to the public than the raw estimate itself.
Thanks John,
I have admittedly not done the analysis myself, but I have not read anything in the literature to suggest that the variance has robustly changed. I’m also not aware of any theory in which one should expect “increased variance” in a warmer climate. If there is a change, I’d intuit that it would be rather small and not an incredibly meaningful diagnostic as far as public welfare is concerned.
Of course, that just an intuition. I haven’t messed with the data myself.
Competing intuitions: higher energy system could imply wider swings; decreased gradient from tropics to poles could imply weaker swings.
I have seen the case that “more energy” means more variability, as if this were self-evident. It’s not self-evident. Only a small part of the “increased” internal, latent, and gravitational potential energy associated with the mean state of the atmosphere is available for conversion to kinetic energy. Moreover, the storm dynamics is intimately connected to the temperature structure and temperature gradients at different levels of the atmosphere.
As you note, decreased baroclinicity in the lower atmosphere implies weaker eddy behavior, though this is itself a function of hemisphere and season. For instance, there is little polar amplification in the summer months in the Arctic. And as a climate model evolves to equilibrium, the structure of the SH meridional temperature gradient changes. However, in the upper troposphere, the equator-to-pole temperature gradient increases in a warming climate, in contrast to levels lower down. This creates increased instability (and increasing atmospheric moisture) that could fuel more intense storms. So there are multiple competing factors.
It’s not really obvious how all of this relates to the “variability” issue, but right now I don’t think we have a satisfactory handle on how mid-latitude storminess might change in a new climate, in terms of frequency or intensity.
Chris, thanks for that precis. In addition to sketching out some of the important features of the weather system, it clearly demonstrates the difference of Physics 101 intuition (billiard balls and oscillators) and an informed intuition!
I haven’t looked at this to have a firm opinion about increased variance.
I would observe that one gets normal distributions by additive combinations of random effects and lognormal (right skewed) distributions from multiplicative effects.
If the variance actually does increase for some relevant subset of data
AND IF the right tail seems to get weighted heavier, then one might look for something with a slight multiplicative effect. The only one that comes to mind might be the drought+hot combination that makes an area really hot, especially if the drought comes from AGW-induced precipitation shifts.
John N-G might comment?
At first blush, the drought+hot combination does suggest a skewed distribution. The variance might be expected to increase for a location that did not normally dry out enough but now does so. On the other hand, places that once occasionally were moist but now become entirely dry would see their variance decrease. Should be a small net effect if averaged globally.
Thanks. To reframe the question better.
In any given place (by season or year/ year) there is for temperature:
a) Mean
b) Variance
c) Skew
d) Kurtosis
i.e., first 4 moments of the distribution, and I think all 4 might be relevant, not just the first 2.
a) increasing mean alone (in normal distribution) just moves distribution to the right.
b) Increasing b) alone just broadens the distribution, still normal.
c) Right skew changes shape of curve, with more frequent hot extremes, but one could get that with same mean and variance, but depart from normal.
d) Increasing “excess” kurtosis makes the distribution more peaked than normal, so lowering that would make it flatter, and move more data towards *both* tails. If one starts with normal, increasing kurtosis reduces the variance, decreasing it raises the variance.
Anyway, it seems to me one would want to look beyond mean and variance to the higher moments and think about whether or not there are physical reasons why one might see these effects, which very well could be different in different places (as John N-G notes).
For instance,
the hot+dry combination might increase right-skew, increase mean, but have the same variance.
the used to be wet, but now hot+dry might well have lower variance, but also might have moved the mean higher and increased the kurtosis.
[One can imagine where hot+try spell kills off the vegetation, keeping it hotter.]
As tamino says, it certainly seems one might need to start at regional and work up, as effects could cancel each other out. One can imagine the areas that will be getting more rain seeing different temperature effects than those getting drier.
Put another way, I don’t know which if any data departs from normal, but if it seems to, one would hope to find physical explanations before one really believes the effect significant.
John M – My guess is that almost all such effects would be found in theory or model a long, long time before they would robustly emerge in the observations. This blog entry is questioning the evidence for a change in the second moment of the distribution of the most robustly-observed climate parameter on Earth, and you’re talking about changes in the third or fourth moment.
I don’t know if moments obey scaling laws, but if they did:
Time required to detect trend in mean: 16 years
Time required to detect trend in variance: >= 50 years, apparently
Time required to detect trend in skewness: >= 156 years
John N-G
yes, that’s why I said:
‘Put another way, I don’t know which if any data departs from normal, but if it seems to, one would hope to find physical explanations before one really believes the effect significant.’
Again, I don’t know what the data says, but I think the bottom line is that when one is looking at curves that *look* normal, it is a good idea to do normality tests and compute the other moments to check. I bring this up because I’ve seen people assume bellish-shaped curves are indeed Gaussians, and then take for granted all the good properties, whereas significant departures may actually give insights about useful effects.
Agreed. You really shouldn’t assume Gaussianity out there on the edge. e.g.: http://www.wcrp-climate.org/conference2011/posters/C39/C39_Sardeshmukh_TH155B.pdf
John N-G: many thanks for that link, interesting, summary on p.10 useful.
I’ll have to spend some time on a few parts, but it is certainly a good reminder that Gaussians are not guaranteed, and in fact, I was interested to see PDFs (as on p.7) that seem to look more like lognormals, at least by eyeball, and if so, then the question arises of doing the log-scale transform to see if the results indeed do OK on normality tests, and hence retrieve the good properties we all love.
John N-G and John Mashey,
I guess you could call this the dark side of the Central Limit Theorem. For a well-behaved, unimodal distribution, the vast majority of the data we have to look at will (by definition) come from near the mode where all distributions will look Normal. You really need a fairly significant amount of data before you can reliably estimate the skew or kurtosis.
One trick I have tried in the past has been to fit to a Normal (zero skew), lognormal (positive skew) and Weibull (negative skew for some values of the shape parameter) and see how much difference it makes. At the present time, we really don’t have enough data even to reliably estimate changes in the variance.
snarkrates:
1) I’ve not had occasion to try Weibull, but lognormal has been useful (for analysis of computer performance benchmarks based on performance ratios.)
2) Even with insufficient data points for a high degree of significance, if one plots data that looks ~Gaussian, and computes a mean and variance, that’s OK. However, if one says anything about skew or tail-weighting, it’s easy enough to compute skew and kurtosis and include them.
While I am fond of graphs, I am wary of statements about statistics that do not actually compute them, but seem to leave it to eyeball.
I’m also fond of Tukey-style EDA, which seems to fit the current state: there may not be enough data, but one should look at it in different ways with the hope that insights will come that help one start looking for better data.
John,
When datasets are small, EDA is really just about all you can do. You can certainly compute sample moments, but can be misleading to interpret, for example, mean and standard deviation as being parameters of a Normal.
It is an interesting exercise to generate Normal, lognormal and Weibull distributed random numbers of various sample sizes and seeing how often you reproduce the sample moments approximate the population moments.
Based on the studies I’ve done in conjunction with my day job, I’m not at all surprised that we don’t see a clear trend in variance, let alone higher moments.
Where can I get time series data on rainfall in various cities, or even states and provinces? I’m trying to work with NCDC, but it’s like pulling teeth to find consistent data.
I think you all are missing the boat, frankly. There is a presumption that the climate we are experiencing at any moment is one of a progression of incrementally warmer climates. This quasi-equilibrium model (like that of engineering thermodynamics) does appear to be useful for the Holocene, but that is an unusual epoch in the context of a partially glaciated planet. Looking back beyond the Holocene, even the modest Milankovic forcings did not yield anything like a smooth monotonic progression.
Once you get out of a quasi-equilibrium regime, the instantaneous behavior of the system becomes dominated by transients, not by the equilibrated state at the given forcing (or an instance of an equilibrated state if multiple solutions exist.)
In particular, the instantaneous state of the ocean surface will be a result of its history far more than a result of the current forcing configuration. The longer the present imbalance persists, the more the upper ocean will depart from any equilibrium. The decadal time scale of each of the basins will combine to produce planetary boundary conditions that are increasingly variable and unprecedented on a year-over-year basis. And accordingly the interannual variability of the large scale dynamics will increase.
This isn’t so much climate dynamics as just dynamics. It’s conceivable that the climate is a special case, but if anyone expects smooth transitions, from where I’m sitting the burden of proof is on them.
I have felt that the last few years have vindicated my understanding in this regard. Yet I continue to see small-signal arguments being made in a context where nonlinearities and regime transitions are increasingly plausible.
In particular, John N-G has argued that because the background trend in Texas is small, the outlier of last year’s extreme heat in Texas cannot, in the main, be attributed to anthropogenic change. This argument is based on smoothly varying statistics. But the very scale of the outlier itself argues against smoothly varying statistics.
Finally, I agree that the details of Hansen’s calculations matter. But I wonder if it doesn’t cut both ways. If an outlying year occurs somewhere like Texas where the background temperature trend is small, wouldn’t it get more weight as an outlier in Tamino’s method?
Michael,
Thanks for the insight, and I’m sympathetic toward the point that a different climate could also come with significantly changed variability rather than just a monotonically increasing trend. There has been a large literature exploring possibility that there is unknown switch in the climate system that could reach a threshold of being activated if we perturb the climate enough by increasing GHG concentration.
As far as I’m concerned though, there is no credible evidence (or proposed mechanism) that would allow us to even start thinking about this in a quantitative manner. The pre-Holocene climate shifts seem to be well accounted for by dynamics of glacial meltoff, freshwater discharge, and the impact on the ocean circulation…all of which is less of an issue in an initially warm climate, and the AR5 generation models give no indication that the overturning circulation will be significantly impacted over the coming century.
We could, of course, hit some bifurcation in the system where we lose all the summer Arctic sea ice or the Amazon forest, which is bad enough, and could possibly transition the climate to a different “solution” on a hysteresis diagram…this to me would represent more of a step-wise jump (akin to a larger bifurcation that you get in a snowball Earth as you gradually reduce CO2 or the solar constant); but ultimately these represent different behavior than “the interannual variability of the large scale dynamics will increase” or that for some reason the climate should be susceptible to more “flip flops” (as in the glacial Heinrich/D-O events), of which I am aware of no observational or theoretical support.
It’s at least more credible than Hansen’s “runaway greenhouse” nonsense, which can be dismissed on rather elementary grounds (without clouds at least), but I think Tamino’s post before about “changing the dice” a bit to land more higher numbers, and possibly a few 19’s and 20’s, is a much more appropriate analogy than the argument that the system behavior will deviate substantially from smoothly varying statistics
“but if anyone expects smooth transitions, from where I’m sitting the burden of proof is on them.”
c.f. the Arctic CO2/temp graphs so fabled in song and story. 12C increases in temperature in a geologic instant. And that’s for the most recent 400,000 years.
Presumably, MT refers here to a system that is “far from equilibrium”, which does not behave in “normal” ways (predictable with Gaussian statistics)
Following is from What happens Far from Equilibrium and Why?(NAS)
//end quotes
How would one go about determining whether a “rare” event is actually a far from equilibrium effect like those described above and not simply a low probability event governed by the normal distribution? (that might have been made more probable due to a shift or even “distortion” in the normal distribution)
Is such a determination based purely on whether the distribution deviates significantly from gaussian?
Horatio,
Remember, near the mean, every distribution looks normal. It is only in the extremes that they look different, and even here you will have one of 4 behaviors.
1) tails converge roughly like a normal (e.g. exponentially decreasing)
2)tails go to zero at some finite value
3)tails converge as a power law (thick tails)
4)pathological behavior, such as bimodality, non-stationarity, etc.
One way to ascertain whether a single event is merely very improbable or indicates a departure from normality is to look at what it does to the moments of the distribution. And look at the moments of distributions with each element in the sample removed (the N samples of N-1 elements each). All this can do is give an indication–to really rule on outlier status for a single event, you need to look at the physics of the process. I am very reluctant to throw out “outliers”. They could be an invaluable gift that gives you a peek at the tails of the distribution.
Food for not particularly cheery thought.
For combined analysis of precip+temperature see the paper in PNAS by Mueller and Seneviratne at
http://www.pnas.org/content/early/2012/07/09/1204330109
sidd
From the main essay:
So if I understand you correctly, the sort of spatial variance that he may have included would be similar to that between different latitudes, with the more northern latitudes having a higher rate of warming due to polar amplification. So even if they have the same variance at a lower latitude as at a higher latitude, if the rate of warming is greater at the higher latitude, this would constitute some of the spatial variance. I believe you are saying as much here in the first part:
… although you didn’t actually bring up latitude. But judging from what you have seen, does it seem likely that the spatial variance they included was largely a matter of latitude? The differential warming of ocean and land? Was it at a finer scale? Or is it even possible to tell?
In any case, it is receiving a fair amount of play. Romm cited it again today, quoting specifically from the passage that states in part:
Krugman Cites Climate Progress on ‘Dust-Bowlification’ In NY Times Piece On ‘Loading The Climate Dice’,Joe Romm on Jul 24, 2012 at 5:33 pm… but fortunately Krugman doesn’t seem to have made a point of it yet.
I agree that very large transients like the Dryas are far off and speculative. I disagree that local trends are especially well-behaved or monotonic. We should expect, on general principles, a noisier and less predictable system.
It seems your disagreement with Hansen is about how to identify variance in outlier events. But local trends are already affected by local outliers. When you’re looking at the bumps the usual statistician’s urge to smooth out the bumps doesn’t help matters.
Hansen’s result is to be expected. That it is upon us detectably is interesting. It seems to me that your quibble will not make much quantitative difference but I’m not convinced it’s right . My main objection, though, is the continued idea that local trends are going to be useful quantities in future. it may be so in some cases but that will require some argument based in physical processes.
Nothing’s more dangerous than a result that is “to be expected” and wrong. ;)
I think you’re conceptualizing that we have this nice stable climate system, and that as we kick it out of equilibrium and it transitions to something else, it’s not going to go quietly, much like a river changing its course.
My dispute with that (strawman?) argument is that we don’t have a nice stable climate system to begin with. Our climate, in several important ways, was stuck between two well-behaved dynamical states.
One example would be the jet stream. Jupiter, a large planet, has many jet streams in each hemisphere, and the number of jet streams is fairly stable. Earth, with its particular size and temperature gradients has 1 1/2 jet streams in each hemisphere in the wintertime, and much of the chaos of winter weather involves the jet streams shifting from a one-jet configuration locally to a two-jet configuration locally.
Another example would be ENSO. At present, the Pacific shifts erratically and frequently between warm and cold phases, but paleoclimate data indicates that, even during the Holocene, there were extended periods when it was stuck in one phase or the other.
The adjustment time of the atmosphere to large changes in ocean temperature (such as with ENSO) is a few months. That is why I don’t think that the atmosphere can tell that the climate is changing on a longer time scale. For all it knows, the climate is stationary.
Because of all this, I agree that the erratic nature of the climate is likely to change as the mean state of the climate changes, but I disagree that any change (or the process of change) is likely to make it more erratic.
While I find the basis of your argument plausible, the conclusion does not follow. There are more than two features of the climate system in the period of climatology, and many of those features have been stable. Given that we are perturbing the system, it is possible that unstable features (ENSO states, number of jet streams) may become more stable, thereby reducing regional climate variability. However, it is also possible that other currently stable features may become unstable, increasing variability. The proper conclusion of your argument without actually going into significant physical detail on various significant features of the climate system is that we do not know whether variability will increase or decrease, but that it is unlikely to remain constant.
TC- Sorry, that’s what I meant…the odds of a more erratic climate are a priori not more than 50%.
“the odds of a more erratic climate are a priori not more than 50%.”
This assumes a new quasi-equilibrium comparable to the Holocene.
First of all, in the Quaternary, the Holocene is unusually quiet. This is the usual counter-argument.
But it misses my point, which is that we are forcing the system hard enough that transients matter. With reference to the typical structure of large scale dynamics, the jet stream may become more “sticky” – leading to the sorts of anomalies we have seen of late. And the places it sticks, i.e., persistent troughs and ridges, may persist for multiple seasons, and then abruptly relocate. This is very much the mechanism that I would expect intuitively.
It’s especially plausible given what we know about the sensitivity of climate to ocean surface conditions. In accelerating climate change, the distinct temperature ranges of distinct ocean basins may very well decouple, leading to unusual large scale flows. Again, these may persist for years or decades before reversing.
The atmosphere adjusts to the ocean on a time scale of weeks, and the ocean to the atmosphere on a time scale of decades. Throw in a decadal scale forcing operating on both, and explain to me why atmospheric trends in particular locations ought to be smooth.
The 50/50 argument is flawed for two reasons. It’s flawed on general principles because it assumes quasi-equilibrium and neglects transients. And it’s flawed on specific grounds because it neglects the decadal time constants of the ocean surface, which is where the specific transients will happen.
“Normal Variation”
— by Horatio Algeranon
Today’s outlier
Is tomorrow’s norm.
To vary higher
Is to conform.
Where is the published literature suggesting that decreased climate variability is a reasonable and expected outcome of this giant experiment? What basis would that have: We’re pumping more energy (forcing) and water vapor (feedback) into a system that is already oscillating chaotically; as a result, oscillation amplitude and chaos are reduced?
OTOH, observations of increased variability due to climate change have been around for years. See, for example, Wilby et al 1997 regarding increased variability in Britain and Western Europe winters; Schar et al 2004, requiring higher variability to explain European heat waves; Peterson et al 2012, specifically regarding extreme events of 2011.
Yet n-g (who is presumably not John N-G) raises an interesting point: Are these observations of a tendency towards increased variability really a symptom of changing dynamic states? That suggests the new dice (1,2,3,4,7,8 or some such) are here to stay.
He is, actually, his handle links to his blog.
I appear to have set up different internet devices with different handles, and I don’t care enough to worry about it.
Following up muon’s point, we have to be careful what we mean by increased variability. If we mean increased variability about a time-varying normal (where ‘normal’ is defined by its purpose of ‘maximum likelihood estimate of the weather’), I stand by my argument above. However, for practical purposes variability might be taken to mean the range of weather outcomes over a given time interval, in which case a time-varying normal essentially guarantees increased variability.
Tamino,
I wonder if you’ve tried looking at Tmin and Tmax separately when characterising temperature variability?
I ask after noticing the highest and lowest on record in the HadCET Tmax data. It appears that Tmax has a propensity towards extreme hot days during Summer, whereas there seems to be a fairly well-defined “floor” for lower temperatures.
Tmin doesn’t exhibit the same behaviour. There is a bias towards extreme cold events around the beginning of the year – late January through March.
In the mean data the Summer Tmax extremes are mostly washed out, though there’s still a signature of low temperature extremes in Winter. The mean data does use a longer dataset however: from 1772 compared to 1878 for min and max. Obviously the particulars of behaviour are likely to be regionally-defined, but I thought it might be an interesting avenue to explore.
And in the meantime, the central US could use some increased variability, at least in the short term:
http://www.wunderground.com/blog/JeffMasters/show.html
Sorry to hijack the thread, but I didn’t know where else to put this link about the misinformation that is being spread about Anthony Watts’ friend, David Archibald testifying before the australian senate. All untrue and both the Institute of World Politics and David Archibald have had a chance to explain or retract.
http://uknowispeaksense.wordpress.com/2012/07/29/david-archibald-addressed-the-senate/
tamino, hi,
Over on a thread at Phil Plait’s Bad Astronomy site, we’re having a bit of a tussle with an AGW denier with the handle ‘Nullius In Verba’. He was referring to a climategate e-mail where the authors were supposedly blocked from publishing in a peer reviewed journal by climate scientist Ed Cook, but he was very cagey about the whereabouts of the paper itself and who the authors were. Here is the thread, and the issue was raised in post no. 129:
http://blogs.discovermagazine.com/badastronomy/2012/07/24/greenland-seeing-unprecedented-melting/
But I managed to dig up the actual draft paper! See my post no. 150 (Steve Metzler).
Question arising: would you be willing to analyse the paper and determine if it should have been allowed to be published as stands? I think this is right up your alley, and would make a great post if the paper turns out to be fundamentally flawed. McIntyre thought it was “Brilliant”, though of course he didn’t provide any analysis on it himself :-)
Best regards,
Steve
Agh. tamino, you accidentally left my e-mail address in that last post of mine. Would it be possible to remove it? Thanks in advance. And… I would be willing to pay for your services to analyse that Auffhammer/Woo paper (whether or not the outcome is favourable to the cause or not), once you tell me how much it would cost me up front :-)
Best regards,
Steve
[Response: Sorry about that, I usually don’t do so — it’s now removed. I’ll email you.]
Steve Metzler, Auffhammer et al is apparently under review with the Journal of the American Statistical Society. It’s probably worth holding fire until the paper is actually published – after all the final paper might be rather different from the MS you linked to.
However I’m surprised you don’t enter into some correspondence with Dr. Auffhammer rather than soliciting analyses/critiques behind his back (but in public!). Dr. Auffhammer is a serious scientist who publishes significant analyses on, for example, the effects of manmade climate change on agricultural yields (not good news), and adaptation costs (also not good news).
If you have questions about his paper, why not communicate them directly to Dr. Auffhammer in the first instance?
You don’t need to publish this, it’s off topic for this thread. We have had WUWT try to undercut Muller’s recent Op-Ed piece by releasing a draft of their analysis of temperatures. I’m seeing some early critiques here and there but one thing that struck me is that Watts and crew are apparently saying that the rate of warming in the continental US is 0.15 C/decade instead of 0.3…And that seems to be right on the global number from Foster and Rahmstorf (2011). Thoughts?
Watts is essentially saying that the raw data (uncorrected for time of observation changes and sensor changes, both important in the 1979-present timeframe) from a subset of stations he chooses arbitrarily shows a 0.15 C/decade trend rather than the NOAA ~3C/decade trend.
He’s reclassified about 3/4 of the stations he’d previously classified using a more recent (and valid) classification scheme.
I say aribitrarily chosen because he starts by chosing those stations that fall into the two highest classifications. This set includes most airports.
But he doesn’t like the (higher) trend that airport stations yield, so he tosses them.
He then essentially proves that correcting station data for known biases such as introducing new sensors that read a bit lower than the old glass thermometers on average changes the trend.
No surprise, this is well known.
He then asserts this proves that the corrections are wrong and the raw data right. Which of course doesn’t follow. But this is what he’s been saying forever.
McIntyre helped at the last minute, and to his surprise, found himself listed as #4 on the paper. He totally missed that Watts was ignoring known issues with the raw data, and describes himself as being “annoyed” for having done so (he was working with the numbers, not where the numbers came from, and because of the literally last-minute help he was given, hadn’t taken the time to read the paper, and hadn’t expected to be listed as co-author).
McIntyre claims that he’ll do a proper analysis. One problem is that Watts hasn’t published his data (which stations fall into which class, and for each station, details on which photos and google map features were used to determine which class).
This was rushed out because of Muller’s op-ed in the NYTimes. Also, Christy is listed as #5 author, and is due to testify at a Senate hearing tomorrow. Watts wanted to make sure he was “primed” with the papers results beforehand, i.e. Watts thinks Christy’s going to testify that we now know US temps are rising at only 50% the rate science tells us. Whether or not Christy’s going to actually do so is interesting, as it would directly conflict with his UAH satellite trends.
Tamino, the walkback by the Great Auditor himself over on Climate Audit is fun to watch, whether or not you want to rip into Watts’ work. At this point, it looks like lucia’s friends, the BEST people (Zeke Hausfather and Stephen Mosher, at least), and probably McIntyre himself are going to rip the paper to bits. Or at least poke some very large holes into it.
Meanwhile, I’m expecting a favorable reception by Curry … :)
> the walkback by the Great Auditor himself over on Climate Audit is fun to watch,
Perhaps. But let’s cut back on the Schadenfreude. I don’t like McIntyre much, but here he immediately took the high road, scientific integrity wise. That deserves admiration, and especially emulation.
… warming in the continental US is 0.15 C/decade instead of 0.3
That’s a dramatic improvement over the old ‘US is cooling’ meme. As late as June 11 of this year, CA was still banging that one: Bottom line is that the US has been cooling for 80 years…
I’ve got Joe Bastardi on the hook over at USA Today if anyone wants to come have fun. http://www.usatoday.com/news/opinion/story/2012-07-31/Joe-Bastardi-WeatherBELL-Analytics/56623728/1
Eeek, the stupid on that thread is scary… I thought about commenting and then decided against wasting time…
Joe Bastardi does realise, doesn’t he, that it’s the 1st of August, and not the 1st of April?
If only we could harness stupidity and turn it into energy!
A lot of fish, and a small Bastardi barrel.
Alas, I think Joe has slipped the hook and gone off to read his tea leaves. We’re left with ideologues, or, as I like to call them, “brick walls with graffiti.”
Note that the Bastardi piece is an opposite view for USA Today’s editorial opinion:
http://www.usatoday.com/news/opinion/editorials/story/2012-07-31/climate-change-record-heat/56624448/1
I do *not* think that’s false balance, but rather clever journalism. I’ve seen it before at USAT and other places.
I read on another blog that Tamino’s issue here means the recent paper by James Hansen should not have been published.
Is that reasonable, or too severe?
[Response: It is not reasonable.]
FWIF: this might be an interesting paper in the context of this debate. Have not seen it discussed much:
Ruff, T. W. and J. D. Neelin (2012), Long tails in regional surface temperature probability distributions with implications for extremes under global warming, Geophys. Res. Lett., 39, L04704, doi:10.1029/2011GL050610.
From the abstract:
… Stations with long records in various climate regimes in National Climatic Data Center Global Surface Summary of Day observations are used to examine tail characteristics for daily average, maximum and minimum surface temperature probability distributions. Each is examined for departures from a Gaussian fit to the core (here approximated as the portion of the distribution exceeding 30% of the maximum). While the core conforms to Gaussian for most distributions, roughly half the cases exhibit non-Gaussian tails in both winter and summer seasons. Most of these are asymmetric, with a long, roughly exponential, tail on only one side. The shape of the tail has substantial implications for potential changes in extreme event occurrences under global warming. …
FWIW, should be FWIW, not FWIF
:-)
Just thinking out loud here. Let’s stipulate that you have showed that a synthetic system constructed as uniform variance over nonuniform trend will appear as increasing variance over a uniform trend. That makes sense.
My question goes the other way. Suppose you had a synthetic system constructed as uniformly increasing local variance over a uniform trend and tried to estimate the trends regionally using an analysis which did not assume a uniform trend. Would the outliers not cause the trends to appear to vary as an artifact of the estimation?
My concern is this. Won’t, say, four sigma hot regional events late in the record cause the regional trends to be higher than neighboring regions? Thus, by using local trends, you are pulling for the null result you got, because the places that had hot outliers would have higher trends, so the hot outliers would appear smaller in your metric?
Hansen leaves us with the impression that we are seeing more outliers than we would expect with linear climate change (fixed variance on top of trends). Let me admit that unlike many people, this is what I expect, so I am inclined to believe it.
Despite my initial reaction, I see you have a point here. My disbelief in the linear model doesn’t constitute a disproof of the linear model. Still, I am concerned that your analysis is such that it could easily reduce the estimate of real increasing variance.
This all said, would you agree that none of it matters in terms of the lesson for policy?
[Response: Yes.]
With respect to baseline statistics, severe hot outliers are increasing to an impressive extent. That’s what matters no matter how you slice it. It’s important not to confuse an academically interesting disagreement with one that has practical policy implications.
[Response: I agree that pretty much any method will be prone to confusing trend and variation. Still I think it’s an issue worthy of closer inspection — as an academically interesting problem. From a practical policy viewpoint, any way you slice it severe hot outliers are increasing.]
Hansen has more discussion, extends baseline to 1931
http://www.columbia.edu/~jeh1/mailings/2012/20120811_DiceDataDiscussion.pdf
sidd
Hansen et al note in their paper
The distribution shown in Hansen Fig 9 for the period 2000-2011 is shifted by about 1 sigma to the right of the distribution for the baseline period 1951-1980.
According to Fig 31 inthis “Jason” paper(pointed out on the “Harbinger” thread), for a normal distribution, such a 1-sigma shift in the mean would increase the probability of an event with an initial 0.001 probability (roughly corresponding to an event that lies > 3-sigma from the mean [probability 0.0013]) by a factor of about 20 or so.
Assuming a direct correspondence between probability and coverage and multiplying the brown area coverage (0.1 -0.2%, which is actually a “theoretical value, at any rate) by 20 would give an area that is 2-4% of the planet surface.
Although the (theoretical) result of 2-4% is a little low compared to the observed result of 4-13%, the “probability increase factor” (20) has put the “>3 sigma” result in the right ballpark. One would not expect theory to match up exactly with observations, at any rate and if the variability has also increased (as Hansen et al claim), that might also explain the discrepancy between expected and observed frequency of >3sigma events.
In the “further discussion” of the paper that Hansen just released, the authors give some results of further analysis (on just the Northern hemisphere)
The increase from 0.4% to about 10% (a factor of 25) would also be consistent with the theoretical probability increase for a shift in mean of the distribution (The factor is actually a little larger than 20 in the latter case because the distribution for 2000-2011 is shifted a little more than 1 sigma from the earlier baseline period (1931-1980).)