I tend to hammer away at the concept of trend. Like many, I’m especially interested in whether, and if so when, trends have changed.
Recent research from Oliva et al. is all about trend change in temperature on the Antarctic Peninsula (AP). It follows in the footsteps of Turner et al., and their common conclusion is that since about 1998, the Antarctic peninsula — so often touted as one of the fastest-warming regions on earth — has been cooling, cooling even faster than it was warming before 1998.
Naturally this has deniers all a-twitter, for instance we are treated to an article by Justin Haskins in theBlaze telling us that:
“Warming on the Antarctic Peninsula has long been touted by supporters of the theory man is destroying the planet by using fossil fuels as proof of the dangers of global warming. Al Gore, the face of the world-is-going-to-end climate movement, has visited Antarctica on at least two occasions to highlight the alleged problem.”
Well, no, warming on the AP has not “long been touted .. as proof …” etc. As for Al Gore visiting the place, I don’t think that has much to do with it at all.
What interests me is the statistics behind claims that the temperature trend changed. I’ll begin by putting some data together, combining the same 10 stations used by Oliva et al. I’ll align them in my usual way [using the pseudo-“Berkeley method”] and form a composite monthly average temperature anomaly for the AP as a whole.
Then I computed annual averages from the monthly averages. This really doesn’t lose any precision in trend estimates (somewhat counterintuitively), and greatly reduces the level of autocorrelation. Finally, I’ve got a time series — annual average surface air temperature — suitable for study.
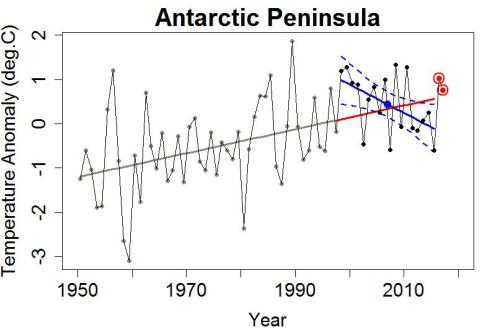
And I can see right away what Oliva et al. and Turner et al. are talking about. The estimated trend (by linear regression) from 1998 through 2015 is rather downward:
Using my combined data set, it’s cooling at 6.4 °C/century, faster even than reported by Oliva et al. and Turner et al. And with p-value equal to 0.03, we have confidence (97%, in fact) that the AP has been cooling over these 18 years.
And it surely doesn’t seem to be warming rapidly, in spite of the fact that it sure was prior to 1998:
Using that time period, the linear regression slope is upward at 2.7 °C/century, and the p-value of 0.007 leaves little doubt about its warming at 99.3% confidence.
Conclusion: the trend changed. With a 97% chance it’s now going downward, almost no chance it’s going upward as fast as it used to be going (back when we were 99.3% sure it was going upward), that’s some solid evidence. Hell, even tamino would admit it’s a trend change, right?
Let’s look closer.
The narrative is: warming fast through 1997, then cooling even faster since 1998. If the last 18 years is the change from warming to a rapid cooling trend, one would expect the 1998-2015 average to be less than it would have been, had that trend change not happened.
We can of course take the pre-existing (1950-through-1997 warming) trend and extrapolate it to the present, to see what would have happened (trend-wise at least) had no trend change occurred:
The big blue dot marks the 1998-through-2015 average of the observations. Notice that it’s above the value at that time for the extrapolated pre-existing trend (shown in red); just when it was supposed to be cooling so rapidly, its 18-year average went up, above expectation.
But that linear regression trend was 97% confidence downward? What’s going on? To get that result, you can’t just change the trend slope from warming to cooling, you also have to change the value of the trend line at 1998. But if you’re allowed to do that, there’s an extra degree of freedom (in the statistical sense) in how you’re modelling the data.
We all tend to ignore the “intercept” in a linear regression, and usually it really doesn’t matter. But when we have a model with two intercepts, we can’t just ignore them both. One of them represents a degree of freedom that won’t go away.
The right way to account for this is the Chow test, and when I apply it to the given data with a breakpoint at 1998, the p-value for a trend change becomes a paltry 0.061. It doesn’t even make 95% confidence, although it does make 93.9% confidence.
Well, at least it’s 93.9% confidence by some pretty strict standards. That’s not a “lock,” it’s hardly “fer sure,” but it’s likely enough that it deserves very serious attention, right?
Let’s look closer.
The breakpoint being tested is 1998. That’s fine if you have a reason to pick 1998. But if you picked it because it looks like there might be a trend change, based on the data you’re using to test for a trend change, then you’re cherry-picking. I often call it “innocent” or “naive” cherry-picking. You don’t need a nefarious purpose to look at 1998-2015 and think “Looks like a trend change … let’s estimate the trend starting then.” It’s natural.
But that means that when there’s nothing really going on, you still get all those previous years to start from and the chance that at least one of them will show signs of trend change is a lot higher than the chance a single random series will show such signs. It’s the fallacy of multiple trials — essentially, if you’re allowed to buy 100 lottery tickets you have a bigger chance of winning, but that doesn’t mean the lottery odds have changed.
When I run Monte Carlo simulations to compensate for the multiple trials, using a 66-year-long total record as I used for Antarctic (from 1950 through 2015), the “maybe impressive” p-value of 0.061 turned into a no-way-not-even-close p-value of 0.67. In other words, there’s about a 2/3 chance of finding a time span at least as suggestive as the one in the Antarctica data.
So no, I do not consider the evidence sufficient to regard cooling in the Antarctic Peninsula as being even likely, let alone established. It’s possible, and only time will tell, but the evidence presented so far isn’t strong enough to stand on its own.
Incidentally, since their studies there’s a little bit more data available, for 2016 and the first three months of 2017. Here’s an update of the previous graph, adding the 2016 and first-quarter-2017 values:
I note that 2016, and 2017-so-far, both came in above the trend line estimated from the pre-1998 data.
This blog is made possible by readers like you; join others by donating at Peaseblossom’s Closet.






It is certainly correct that a fit to temperature data should be a continuous function, since temperature is an indicator of system energy content (and energy is a conserved quantity). How do we make that argument to a non-specialist audience?
Tamino, how will the first figure look when you include 2016? Thanks.
Another case for the Chow test.
Fascinating. Let’s see if I’ve got this right. The analysis shows that the Antarctic data may be plausibly be accounted for either as a trend change, or a ‘pause’ resulting purely from unforced variability? And the data from the last year and a half, though still far from definitive, is suggestive that the latter hypothesis could well be the correct option?
Thanks, Tamino. By the time you presented the data from Oliva et al, I was already thinking, “Why pick 1998. Is that cherry picking? What about nonphysical discontinuities in the temperature? What would a trend point analysis show? ”
Before reading your blog, I wouldn’t have known to ask such questions.
That you went off in directions I didn’t expect (degrees of freedom, the Chow test) nuts tells me how much more I have to learn.
Thanks Tamino, for another fine explanation of the proper use of statistics for us statistical semi-literates.
General comments:
– it was well explained that the apparent 97% downward trend since 1998 could have been known to be nowhere near that significant even in 2015
– with the later 2 data points it is certainly clear now! Someone might care to do the official stats in case my eyes are deceiving me from the final graph, but I doubt it (but unlike the fake sceptics, I am open to the possibility)
– and also a good explanation of “naive” cherry-picking. Most of us are more familiar with the cherry picking shown in the Blaze article (“deliberate?, Dunning-Kruger”?), so it is a good reminder that it can also be more innocent/subtle.
Reblogged this on Atmosphere and climate over Larsen C and commented:
This is an extremely interesting consideration of the validity and robustness of trends estimated from limited numbers of data points. The jury is still out on the magnitude and even direction of temperature trends on the Antarctic Peninsula – clearly the need for further research and data collection is ever more pressing.
Hey Tamino, could you add the trend and uncertainty in the trend from 1998 once you include the latest data?
Great post. Just asking: you’ve done trend point analysis in past posts; is it possible to see if there have been any trend changes in the full record? Heck, in some ways, I expect a reduction in warming rate in Antarctic waters, due to high ice melt due to global warming effects – it would be interesting if this could be seen with trend point analysis. I have no idea how to do that.
Thanks.
Isn’t the case for a change in the trend even weaker than you say? After all, there are many different areas across the globe whose temperature is described by trend+noise? I’m not a statistician but it seems to me that if you have enough areas of trend+noise it is likely that some will have an apparent period of negative trend.
Ah…the old pick a local max and start the analysis from there trick!
What would deniers do if they didn’t use that one?!
Looks like they missed an opportunity to start with the highest anomaly in the record around 1990. It might not have given them such a dramatic negative trend, and they wouldn’t have had such a neat link to the famous canard, but they would have been able to say that the AP has cooled for 25 years!
“They” = pseudo-skeptics, not the authors of the papers linked in the OP. Don’t mean to impugn Oliva, Turner et al.
As for the OP, I have observed over many years that physicists can be, as tamino notes, “naive” about regression and inference.
Many also have naively searched for meaning in the “pause” data. I’m not saying there isn’t any, but you don’t get there by _assuming_ a subset of data is significant and then looking for reasons why. It just may be noise.
All this reminds me of the Stats 101 exercise where you ask students to generate series of 100 heads/tails cognitively versus with actual coin flips. The two series are easy to reliably differentiate as actual coin flip data shows apparent “meaning” in runs whereas cognitive series usually try consciously avoid runs as they appear not random to the eye. This however makes them observably and measurably nonrandom in actuality.
This cognitive illusion is very powerful and hard to overcome. One needs to “fly on instruments” (stats done correctly) to avoid crashing because of vertigo. And this, of course, is why deniers use it constantly–usually on purpose, and even scientists get fooled.
Looking for and not finding graph of average albedo of the Calcite Belt, 1950-present .
Welcome back!
Tamino-san, if you get a chance, please let me know if I made any mistakes here, at least in the statistics part:
http://bartonlevenson.com/ISK/ISK.html
Liang causality is strictly superior to Granger causality. I suggest making the change.
Benson-san,
I have looked up Liang’s papers, but I can’t make head nor tail of how to actually compute the results. He says it’s merely a matter of sample covariance, but I can’t seem to make it through his symbolism. Could you give a succinct algorithm?
Barton, look in to methods section of the paper linked in the following comment, about the causal connection between CO2 and global temperature. Equation 2 appears to be the means of determining the information flow using expectations and second partial derivatives. If that is not enough, I suggest contacting the corresponding author of that paper for the additional details required.
Luck!
“On the causal structure between CO2 and global temperature”
https://www.nature.com/articles/srep21691
explains and uses Liang causality, called IF, information flow, in the paper.
As a separate matter, the results are interesting although the main 2 results are not surprising.
Where can one find a source for the 2016 and 2017 so far anomaly numbers?
Where I looked you needed an account to get in, but the KNMI climate explorer can access some data if you fill out the fields correctly.
https://climexp.knmi.nl/selectstation.cgi?id=someone@somewhere
Make sure to delete any fields you aren’t using.
Its just the plain good ole “Pause”, “hiatus”, “Global warming stopped” since 1998 Trick, only applied to annother dataset.
Don’t scientists normally claim that 17 years is needed to see the trend rise over the noise for Global temperatures? For a small area like the Antarctic Peninsula more time would be required for the signal to escape the noise. An 18 year record is too short for a local area.
As expected, with more data the signal starts to appear again.
[Response: The required time depends on the strength of the signal and that of the noise. Specific time spans don’t seem like a very good idea.]
Michael: the length of time needed is a characteristic of the data, not of the methodology. Bob Grumbine has a good post on that here:
http://moregrumbinescience.blogspot.ca/2009/01/results-on-deciding-trends.html
That 17 years comes from a paper by, IIRC, Ben Santer, who showed that a period of at least(!) 17 years is required to find a signal within the noise of temperature records.
Santer et al, 2011, PDF–as best as I can do on my phone, anyway:
https://www.google.com/url?sa=t&source=web&rct=j&url=http://muenchow.cms.udel.edu/classes/MAST811/Santer2011.pdf&ved=0ahUKEwj2vPecqOHTAhVr04MKHX76D2AQFggfMAA&usg=AFQjCNG58b9umiobTzAXQ_51ULrSi61rMg&sig2=Xheb6i30zPG9BVCrRGq-FA
Hope that works…
The papers recommends 17 years “at least” in the abstract, but in the conclusions recommends “multidecadal” periods to determine an anthropogenic signal from the noise in lower tropospheric temps.
Abstract:
…Our results show that temperature records of at least 17 years in length are required for identifying human effects on global-mean tropospheric temperature.
Conclusion:
…The clear message from our signal-to-noise analysis is that multi-decadal records are required for identifying human effects on tropospheric temperature.
http://onlinelibrary.wiley.com/doi/10.1029/2011JD016263/full
Unfortunately, ‘skeptics’ never read past the abstract.
Thanks for all the replies.
I understand that the time needed depends on the data. For example, the Mauna Loa CO2 record does not need as long a time as global temperature.
My point is that in general for a small area at least 20 years is needed and you probably need thirty (or more for such a small data set) years to claim a real change. SInce in this paper they only used 10 stations (!!??), their time period is much too short unless they provide data that the area is unusually stable in trend. The result they found is what would be expected from random variations in a small data set. There are thousands of small locations that can be cherry picked, this one happened to be interesting.
The original analysis used 50 years of data which is much more likely not to be affected by random variations.
From the abstract of Santer et al 2011, “Separating signal and noise in atmospheric temperature changes: The importance of timescale”:
“Our results show that temperature records of at least 17 years in length are required for identifying human effects on global-mean tropospheric temperature.” http://onlinelibrary.wiley.com/doi/10.1029/2011JD016263/full
Of course this findings have no meaning for a small part of the world in the Antarctic. There the needed timespan is quite probably waay longer – it depends again on the characteristics of the data from there.
As I said; the good ole “No warming since ’98, 2002, 2002 2005 etc.” scam again.
What are the odds that 5 years in a row would be below the trend estimate? Is that even meaningful?
Assuming white noise, 1 in 32.
Now “what are the odds that we will see 5 years in a row somewhere in a longer series?” is a completely different matter. Tamino and many others have taken extreme pains to point this out over the years.
On the subject of trend analysis, if you have time, in a future blog post it would be great if you could take a look at this new article on Arctic sea ice trends since 1901 https://twitter.com/1ronanconnolly/status/861295825808486400
For context, in addition to Willie Soon, the other two authors have this website http://globalwarmingsolved.com/start-here/
The scientists then applied a statistical technique, known as a Mann-Kendall test, to look for any point within the time series where the size or direction of the trend changes.
Using this method, they found such a point occurred in late 1998 to early 1999. Before this, the stations recorded an average warming of 0.32C per decade. But afterwards, the trend turned negative, showing 0.47C of cooling per decade until the last measurement in 2014.
By repeating the analysis without 1997 or 1998, the authors satisfied themselves that the switch from warming to cooling trend was not an artefact of the extreme El Niño conditions.
No cherry picking to find a trend here?
A Mann-Kendall test is just a nonparametric test for a monotonic trend. “Nonparametric” man that it doesn’t assume a normal distribution–nonparametric tests are generally less powerful.
It is, AFAIK, not a “magical” test that can “objectively” identify acceptable points where the trend changes. Correct me if I’m wrong.
I wish you could edit posts.
Anyway, so, I’m neither convinced that (1) this doesn’t involve cherry-picking, nor (2) this overcomes the “jumping trend” problem.
Angech,
Could you please post an excerpt from the paper that describes how they did this?
Basically, if they used any method to find the most promising part of the overall series, all further analysis of the chosen cherry needs to be corrected for multiplicity. Any statistical analysis performed on the cherry that does not account for how many possible start and end positions were originally available is not simply misguided, but deeply wrong.
If the cherry-finding technique itself produces a measure of significance that includes a correction for multiplicity, that is different, but you have provided no evidence that this is the case.
The Mann-Kendall test does not appear to be a method for finding out whether a long trend includes statistically significant subtrends [Response: You’re quite right.], at least not in the links I have followed. It is described as a test for assessing whether a monotonic trend exists.
http://vsp.pnnl.gov/help/Vsample/Design_Trend_Mann_Kendall.htm
“The MK test tests whether to reject the null hypothesis ( Ho ) and accept the alternative hypothesis ( Ha ), where
Ho : No monotonic trend
Ha : Monotonic trend is present”
Even if they had done their stats correctly, they would still have the problem that the start of their trend requires a sudden inexplicable breach in the prior trend. As shown in tamino’s graphs, their trend begins way above the main trend line. The jump to the start of their trend is entirely non-physical and unexplained. The improbability of their trend being due to chance, even if calculated correctly, would need to be balanced against the impossibility of their trend starting at a magical energy-creation point.
Could you please post an excerpt from the paper that describes how they did this?
No, sorry. I must have reached a link through Tamino’s references but now find they have large costs to access whereas I just linked in. I agree their method picks the best start date for a change of trend but there are numerous dates pre and post 1998 which would still show downwards trends of greater or less significance
This is a phenomenon well known to particle physicists: They comb through their data looking for “bumps” that might indicate some sort of particle decay or resonance and then apply (hopefully) reasonable and physically justifiable filters. The result is a whole helluva lot of bumps–most of them spurious. They compensate for this by requiring 5 standard deviations of significance before they publish. Interestingly, a certain string theorist whose initials are LM does not understand this.
Angech,
You really don’t understand stats at all, do you?
Angech:”…but there are numerous dates pre and post 1998 which would still show downwards trends of greater or less significance”
Uh, dude. Come on, Angech. You’re almost there. What can you conclude from the fact that you can cherrypick many different short durations that show behavior different from the overall trend?
Isn’t your analysis compatible with the Turner et al. paper as it suggests the so-called absence of warming is consistent with natural variability? As natural variability should been found in the rest of the temperature data the conclusion of a trend being natural variability seems to be compatible with the conclusion of no established trend change.
Is the dispute then a dispute about the language of analysis. How to call such a short period which seem to have no warming, but is not statistically enough for a trend change?
[Response: I don’t know, but I do know this: you do NOT say “cooling at a statistically significant rate” (as in the abstract of Turner et al.) when it just ain’t so — like now.]
The real problem here is that the whole line of reasoning is spurious, as Tamino points out earlier in the post before he even starts doing statistics.There’s absolutely no scientific validity in choosing a particular region over a particular time and pretend that trends there (or lack thereof) either support or refute the hypothesis that adding heat to the Earth system will cause it to change its temperature. As Tamino shows, the contention on The Blaze was false, but even if it were 100% true it wouldn’t undermine the First Law of Thermodynamics not a whit!
The Blaze apparently exists to lie.
“There’s absolutely no scientific validity in choosing a particular region over a particular time and pretend that trends there (or lack thereof) either support or refute the hypothesis that adding heat to the Earth system will cause it to change its temperature.”
Ummm. scottdenning
If trends and no trends in a chosen region and time can either support or refute a hypothesis you cannot make a hypothesis?
Extended your assumption implies that trends in regions and times in general do not have scientific validity.
Choosing any place and time will show trends or lack of which can scientifically support or refute a hypothesis.
What needs to be done is to contrast and compare to bigger pictures at other times and places to confirm or refute.
A cherry pick [pretence] is always scientifically valid at that one time and place, just not really.
Your reading skills are less than mad. “heat to the Earth system will cause it to change its temperature.” If you want to refute that hypothesis, you need take the whole earth over an extended period of time.
As stated in Tamino’s excellent book, “Understanding Statistics,” a quintessence of statistics is separating signal from noise; and then making sure you are not fooling yourself. False positives are especially pernicious.
Another way to state this might be an erstwhile gambler who goes to a casino with $1,000 and quickly loses $500 in the first hour, then hits a ‘winning streak’ in the second hour and gets back to $1,000. If he starts his ‘trend’ line right at the point when he starts winning, it sure looks like he had a good night!
A repost of Singer’s arguments from 2006 on WUWT has shown up and this post of yours refuting it seems an apt place to start.
Wanted to just mail you what I have so far as a starting point but I don’t think I have your e-mail and the fool where I posted it just now has some issues. I did link back to your work there … I might refine what I did so that it is actually polished up rather than simply reasonably complete.
http://boards.fool.com/Message.asp?mid=32711832
I also asked whether there was any change in the paper since 2008 and so far don’t see any, Dr Singer may not even have been involved in posting it. The usual gish-gallop but I thought it possible that you might want to guest a rebuttal on SkS or re-do one here?
I hope this is appropriate.
Thanks
BJ
Ah… and you won’t have my e-mail. bj*DOT*chippindale*AT*gmail*DOT*com
Tamino, I used your constructed annual AP time series 1950-2015 and carried out a Bayesian change point analysis on it. I tested it for 0, 1, 2 ,3 & 4 change points with DIC as the measure of model fit (it penalises for model complexity). I found for your time series that really no model other than the 0CP model has a DIC score sufficiently lower to be worth ‘the extra complexity’. I was concerned at the relatively few data points and decided to fill out the time series by interpolation and made the same graph into 1,070 time points and tested it also. The 1CP model is barely any better than 0CP and has the CP in mid 2012 which really is not a valid CP towards the end of the time series as it lowers to the 2015 value.
In summary, Bayesian CP analysis would class this time series as a 0CP model with a median slope of 2.68C/century and 95% equal-tailed credible interval of 1.5-3.87C/century. It would be interesting to do a similar study on the monthly AP aggregated values.