Desperate for a “Pause”

When it comes to temperature at Earth’s surface, with 2014 the hottest year on record and 2015 on pace to exceed even that, things are getting hot for those who deny that global warming is a danger to us all.

In their scramble to find something that looks like global warming has somehow “paused,” they seem to have settled on one particular data set with which, if you wait until just the right moment to start looking, it looks like they want it to look.

The data set du jour for deniers is the lower-troposphere temperature record from RSS (Remote Sensing Systems). It’s an estimate of the temperature in our troposphere, the lower layer of earth’s atmosphere, based on satellite measurements (but not direct temperature measurements). The usual approach is to show this data — but only part of it — then just say “no global warming” loud and long.

The latest incarnation claims that there’s been no global warming for 18 years and 5 months, meaning all the way back to the beginning of 1997. Let’s look at temperature data for the lower troposphere ourselves. But instead of the satellite data, let’s look at temperature data from actual thermometers. The satellites are great, but they measure microwave brightness, not temperature — we have to deduce how hot it is from the microwave data. That’s an extremely complex problem, and splicing together all the records from all the different satellites (there have been many) is a delicate issue. All of which is part of the reason the different groups doing so don’t agree on exactly how, or what the result is, and so often the satellite temperature data have been adjusted and revised.

For decades various organizations have been sending thermometers (and other weather instruments) up in balloons to measure the conditions at altitudes throughout the atmosphere. This has enabled us to combine the results from the long history of balloon-borne data into estimates of the temperature in earth’s troposphere.

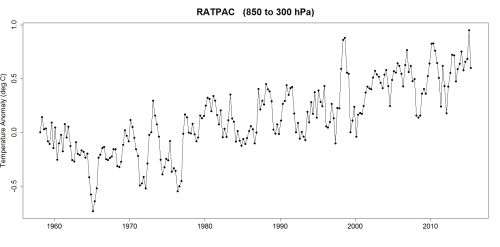
I have in the past studied the HadAT2 data from the Hadley Centre/Climate Research Unit in the U.K. Unfortunately that data has not been kept current, it only goes as far as the end of 2012. But there are others, including the RATPAC data designed specifically for climate study and which is current through this year. The data they report which is most relevant, covering pressures from 850 to 300 hPa, is in fact for the heart of the troposphere.

Not only do these data reflect the measurements of actual thermometers, they also cover a longer time span — back to 1958 — than the satellite data which don’t start until about 1979. So here they are:

This definitely does not give the impression of any pause in warming. Of course, the truly relevant question is, has there been any real change in the trend since 1970?

Let’s use least-squares regression on the data since 1970 to see what the trend is since then:

It’s clearly upward, in fact it’s going faster than the surface temperature data. Now let’s compare that to what’s happened since 1997. Again I’ll compute a least-squares regression line and add it to the graph, but that first line was in blue so I’ll plot this one in red:

Some of you may have a hard time seeing both lines, simply because the trend-since-1997 line is right on top of the trend-since-1970 line. Their really isn’t any difference in their warming rates. If you’re color-blind it might be hard to see that there are two lines plotted, not just one.