We recently pointed to another example of mathturbation brought to you by Anthony Watts, courtesy of Pat Frank (author of this travesty in E&E). A reader asked, “could someone post a paragraph or two about the specific flaws in the WUWT presentation.”
OK.
Actually, a number of comments have pointed out numerous, serious flaws already. But let’s take a close look at Frank’s model. His post is about fitting a curve to global temperature data, specifically those from NASA GISS and HadCRU. The chosen curve fit is a combination of a linear increase and a sinusoidal waveform. We’ve seen this before. It’s easy to fit a waveform to data. It’s not so easy to establish that the data are actually cyclic.
But Frank doesn’t even attempt to do so, there’s no statistics at all. Such effort would be futile, because of the simple fact is that there aren’t nearly enough “cycles” to show that global temperature is following a cyclic pattern. Even if there were, establishing cyclic behavior is very tricky.
Nonetheless, Frank charges ahead. He fits a linear-trend-plus-sinusoid model and gets this:
He then declares “The unfit residuals are shown below the main plots. A linear fit to the residuals tracked exactly along the zero line, to 1 part in ~10^5. This shows that both sets of anomaly data are very well represented by a cosine-like oscillation plus a rising linear trend.” As another reader pointed out, if you fit a linear+sinusoid model to some data, then the residuals will have zero linear slope. Necessarily. Whether the model is any good or not.
Let’s give the model a test, shall we? The “model” is that global temperature is following (and will follow!) a linear trend plus a sinusoid. Let’s do a classic test: estimate parameters by fitting the model to most of the data, then see how well it can predict what follows. Frank uses both GISS and HadCRU data, but let’s focus on GISS (the HadCRU data is just more of the same). We’ll compute the best fit for this model to GISS data from 1880 to 2000 (actually the end of 1999), then extrapolate the model through to 2010, giving this:
This is what the residuals look like:
Does the model prediction have any skill? You make the call.
Let’s try a different model: that since about 1975, global temperature has increased approximately linearly. Again, let’s fit this model to data from 1975 to 2000 (actually the end of 1999), then extrapolate the model through to 2010, giving this:
The residuals look like this (plotted on the same scale as the residuals from the previous model):
Which model did better? You make the call.
We can even fit Frank’s model to all the GISS data, then train a skeptical eye on the residuals. Here’s the model fit:
Here are the residuals:
Unfortunately for Frank (and the many other linear+sinusoid mathturbators), the fit really isn’t very good. But it does have zero linear slope!
Let’s try another model. Suppose we hypothesize that since 1880, global temperature has followed four straight lines: one up to 1919, another from 1919 to 1946, a third from 1946 to 1974, a fourth from 1974 through 2010. The model looks like this:
I will not pretend that this model is especially insightful, or that it will continue throughout the remainder of the 21st century, or that it enables us to estimate climate sensitivity. I certainly won’t claim that it gives us any insight about the danger (or lack thereof) we might face from a doubling, or a quadrupling, of CO2 levels.
But I will state that statistically, it’s a way better model than Frank’s. Here are the residuals:
Better or worse than what Frank got? You make the call.
We can also compare the models using the Akaike Information Criterion, or AIC. Frank’s model gives -222.72, the 4-line model gives -255.07 (yes, I included the three change-point times as parameters). Since lower AIC means a better model, the 4-line model wins. In fact, the difference between AIC values can be used to compute “Akaike weights” to be used if we want to compute weighted estimates combining information from both models. Relative to the 4-line model, Frank’s model has an Akaike weight just a smidgen less than one out of ten million.
Frank’s model has no physical basis. It ignores the known physics of climate including greenhouse gases, sulfate aerosols (both man-made and natural), solar variations. It fails the simplest test of predictive skill, miserably. It fails comparison to a ridiculouly simple multiple-lines model, miserably. His use of results to estimate climate sensitivity is, not to put too fine a point on it, laughable.
In other words, it’s perfect for the WUWT blog.
Open Mind 
Any chance Frank will come here and defend his work?
What, and lower himself by associating with those engaged in the conspiracy? OT: Are you the b_sharp who posted at Darwin Central? Carolinaguitarman here.
I’ll be damned, Frank did show up to defend his work. It doesn’t look like he’s a statistician though, so his kahones must be huge to go up against a professional. Or it could be Dunning-Kruger.
OT: CG, yup it’s me. Find me at LGF.
Not really :)
(the term “own goal” comes to mind)
Not that there aren’t a million ways you can pick this apart, but I’ve always thought some sort of number-of-runs test was the most intuitive way to attack this sort of fit (the decade-long run of positive residuals in such a noisy data set is somewhat unlikely). That or plotting the fit along with a moving average to show that it only looks like an OK fit because the data’s so noisy.
Do residuals necessarily have a zero slope? It seems like that’d be dependent on the fitting algorithm. I understand that that’d usually be the case, but if I fit the function y=a to data with some nonzero correlation I’d get a nonzero slope in the residuals.
If you fit a function with a linear trend component then the residuals must have zero slope. Otherwise, you could improve the fit by incorporating the slope of the residuals into your original fit.
Just out of interest, I noted that Pat Frank “held out” the HadCRU data from 1850 to 1880. Any chance of a plot of his full model against the full HadCRU temperature series, and a look at the residuals?
I think it’s safe to say that Frank has taken the place of Goddard as the WTFWT resident “idiot who thinks he’s doing science” crown.
You mean we can expect the “Frankly science” blog soon, I guess?
Reminds me of this National Post article which was constructed entirely around a graph that is now mysteriously missing from the article. But I took the precaution of copying the graph; here it is. The article was written in October 2008 exactly at the point of a minimum, and some mathturbator fitted a really high order (9th I think) polynomial to it.
Mathturbation
Grips the nation.
The brain is on
A long vacation:
“I have a theory and it is mine
It serves me well most all the time
I’ll be quite frank
It is quite swank
“My latest curve fits to a T —
A polynomial to the tenth degree.
The global trend
Has downward bend
A basic fact that’s plain to see.”
Lorne Gunter isn’t known for his honesty or accuracy.
Zach says:
The residuals necessarily will have zero slope IF THE FIT INCLUDES A LINEAR TERM (which your example doesn’t). The proof of this is essentially by contradiction: If there were a linear trend left in the residuals, the fit could be improved by incorporating this linear trend into the linear term in the original fit, which contradicts the notion that this was the optimal fit incorporating a linear term.
Since a linear term and a sin are not exactly linearly independent, you might expect to have a leak between the two.
Yvan: You may be right about that. I tried to investigate it numerically in Excel, but its Solver is pretty annoying…so I would be better off using MATLAB’s nonlinear least squares fitting routines.
At any rate, even if true, the extent to which the residuals do or do not turn out to have zero slope probably is still not a good indicator of the fit itself…but more an indication of this linear independence issue.
I was just making a point about some subtleties that are often forgotten. If you fit two function that are not completely independent, you will mess your results.
Fitting without physical model might be ok in many circumstances, but you must understand the scope of such analysis.
I think it is interesting how they use ‘explains’ instead of ‘model’. As in:
“Figure 1 and Figure 2 show that to a high degree of certainty, and apart from year-to-year temperature variability, the entire trend in global air temperatures since 1880 can be explained by a linear trend plus an oscillation.” — Pat Frank
It’s almost as if they think ‘model’ is a dirty word, to be used disparage other explanations.
Frank’s model has no physical basis.
I think this is a very important point. If we take a very simple example of, say, a pendulum swinging, then it is very easy to explain and predict the periodicity of the swing of the pendulum by reference to the force of gravity acting on the pendulum.
With the glaciation-deglaciation cycles one can also make a good case for linking this to Milankovitch cycles in the Earth’s orbit, the consequent changes in springtime solar radiation, leading to albedo and other feedbacks.
I also think this is where computer models can be really helpful. If you take a controversial oscillation such as the Atlantic Multi-Decadal Oscillation (AMO) then it is going to be a very long time until we have enough observed periods of the AMO to confirm its existence, *and* we may be disrupting it to a greater or lesser extent via global warming.
However, an AMO exists in (some?) climate models, which can have control integrations lasting thousands of years. One can look at the model output in a way to understand what is creating the oscillation in the model, and so target real-world observations to particularly useful locations. One can also perform experiments with the model to see what happens if you take away certain elements of the real-world, and change the oscillation.
To further your point, an important use of models is to calculate how much warming can be attributed to each physical factor (with appropriate ranges). It is very important to ignore this point if you want to claim “it’s the sin”, “it’s cycles in the [Atlantic/pacific/duck pond]”, “it’s my anties farts” or what ever. We know everything contributes but there are limits as to how much or little warming can possibly be attributed to each physical fact. Ignore the physics and you don’t have to worry about this.
If we gave mathturbation to describe the indiscriminate use of matlab/R/etc. Then we also need something like physlatio for the upside-down, unproductive – although enjoyable for some – approach to physical facts.
It is very important to ignore this point if you want to claim “it’s the sin”,
Well, Romm is predicting Hell and High Water.
Yeh, yeh… sometimes I think the iPhone knows better than me!
Technical question: Is the AIC used the AICc?
[Response: No. Of course, the comparison isn’t close enough for it to make a difference.]
@b_sharp
Two chances of that: slim and none. But if someone at WTFUWT alerts him to the presence of these two tamino posts, there is a good chance he will post a ‘rebuttal’. And you can’t comment (well, not effectively anyway) over there because you’ll just get ‘shouted down’ in the comments. I’ve never seen a comment that represents the real science behind AGW that a single WTFUWT commenter ever agreed too. That would be inconsistent with their worldview.
Anyway, I just checked WTFUWT, and Frank’s post already has 6 other new posts on top of it. And while there is a reference to a tamino article in the comments, it’s not to either of these articles. That’s how they operate over there. Yesterday’s post is soon forgotten, and on to the next bit of inanity.
Tamino, could you add a graph containing the results of Frank’s model a hundred or so years prior and after the known temperature readings? I.e. from 1750 to 2100? I like to know where the temperature came from and where we’re heading, perhaps accompanied with reconstructed and IPCC projections. I could do that in Calc ofcourse, but it might give additional ‘insight’ to the readers.
There’s a shitload of bizarreness in Frank’s post: for example, after substracting the “cycles” he computes the 1880 – 1940 warming rate and then computes 1960 – 2010 rate: he then asumes that the effect of GHGs is the difference between them. Why? Because he asserts that the 1880 – 1940 rate is the rate corresponding to “LIA recovery” and GHGs effect “kicked in” around 1975! So his “calculations” amount to:
– Assuming that 0.65 ºC of the increase in T is due to “LIA recovery”, and that the rest of it is caused by GHGs
– Assuming that 100% of the increase in forcing immediately translates into T (shall we call it a “zero-box pseudomodel”?)
– Dividing that fake “increase attributable to GHGs” between the increase in forcing.
With this method we can atribute global warming to almost anything we can imagine and obtain any numbers for sensitivity. Let’s assume that the Russian Revolution initiated a trend of 0.4 ºC/decade that caused a 2.00 ºC increase in avg. T between 1960 and 2010; then our delta T attributable to GHGs is about -1.2 ºC, which divided between a ~1.8 Wm^{-2} (looking at his Figure 5) increase in forcing equals a sensitivity of -0.67 ºC·m^2/W. Wow, the IPCC got the sign wrong! Undoubtedly Earth is telling us that we should emit more CO2 in order to offset communism-caused warming!
The fact that most of the WUWT comments I have read do not spot the obvious flaws in his reasoning and uncritically accept Frank’s ridiculous thesis because it says what they want to hear is just one more example that WUWT’s purpose is to feed ridiculous nonsense dressed with some graphs and numbers to look “solidly sciencey” into the mouths of ignorant tin foil hat wearers. A fact that won’t surprise anyone, of course.
Wow, that was quite epic.
Kartoffel wrote on June 3, 2011 at 2:14 pm
quote
There’s a shitload of bizarreness in Frank’s post: for example, after substracting the “cycles” he computes the 1880 – 1940 warming rate and then computes 1960 – 2010 rate: he then asumes that the effect of GHGs is the difference between them. Why? Because he asserts that the 1880 – 1940 rate is the rate corresponding to “LIA recovery” and GHGs effect “kicked in” around 1975!
unquote
Tamino kindly calculated for me the CO2 forcing for the two 20th century warming periods (approx 1910 t0 1940 and 1970 to 2000). The first was .25 watts/m^2 and the second 2 w/m^2. During the second warming, the anthropogenic warming (assuming all the CO2 increase is anthropogenic) is 8 times its effect in the first.
So as a first approximation the assumption of a 1975 CO2 kick-in seems reasonable. Why the screamer?
JF
Julian: “LIA recovery”. Where’s the physical mechanism?
Thanks, Tamino and all of the other posters who took time to help. I’ll read this carefully.
MLH
This is off topic, but the last few days there has been an annoying ad showing up on your blog under the first post on each page called ‘End the Delusion’. It is an advertisement added by Google’s Adsense program. Seriously, I don’t think you want it on your blog, it goes to http://www.heartland.org.
Tamino, thanks for this post. They don’t let me post at WUWT anymore. You posted what I would have said in the WUWT comments section and then some.
The volume of nonsense over there is so large that it is hard to keep up with it with the rebuttals. The combination of confirmation bias and the Dunning Kruger effect is overwhelming.
But he had nice graphs! And it sounded so convincing. Surely all that effort couldn’t have been wasted?
On a serious note, I look after a large class of 1st year uni students, and we have two 15-question multiple choice tests in 1st semester. I did some analysis of performance in test 2 vs performance in test 1, and if you looked at the results naively, you might conclude that the students who performed worst in test 1 were most likely to improve in test 2. It would be easy to frame a convincing argument to this effect, with nice graphs and all. You know, “students stung into action by bad marks work really hard and improve”.
But only if you ignore the underlying mechanism. In mcq tests, there is luck. And for weaker students, luck is a bigger factor in their marks.
Say a sub group of students know 5 of the 15 questions, and could reasonably expect to guess 2 of the remaining 10, for a score of 7. But some will be unlucky, and guess none, (and end up with a score of 5), while others will get lucky, and guess (say) 4, and end up with a score of 9. This happens in test 1. Now along comes test 2, and the unlucky student is unlikely to be as unlucky as before, so his/her mark is pretty likely to go up. So it looks like they’ve improved – but it was just chance.
You have to be rather brutal with your pet ideas sometimes, and just recognise, that, attractive as they seem, there is no evidence to support them.
Tamino – not a post but a suggestion for a topic. One of the indicators that the future is not as rosy as hoped for by the “CO2 is good for us” crowd would be a change in trend for world mortality rate. The question is how long would we have to have an upward trend to be confident that it isnt noise?
[Response: It depends on the noise level, which I’d guess (just a guess) is pretty small.]
Duane Gish would be proud.
Anthony’s beloved, would-be, giant-killing surfacestations report was ‘disappeared’ within days too.
Winston Smith doesn’t come into it.
I recall a previous effort by Franks – a bit of pseudo-science called A Climate of Belief that Skeptic.com, which supposedly has debunking of pseudo-science as it’s aim should have known better to publish. It doesn’t look like his reasoning has improved. What did Gavin say about that one? Something about using a toy model that had no resemblance to a GCM. GCM’s, modelling real physics are constrained by that – Franks’ toy model was unconstrained by anything except an intent to misrepresent real science and present the ‘right’ message. It was clearly aimed at the susceptible ignorant yet even an non-scientist and non-mathematician like me could pick holes in it.
How about this one?
http://bit.ly/cO94in
[Response: It doesn’t even fit the data, past or present.
Stuff like this makes the “Leprechaun theory” look sophisticated. It’s not even mathturbation, it’s just graphturbation.]
Here is the correlation: http://bit.ly/f7VYQH
[Response: Big fracking deal. The correlation for the 4-line model is better — way better. In fact, the correlation between annual average global temperature and Mauna Loa CO22 level is better.]
Mind you in the graph http://bit.ly/cO94in almost all the observed data lie in the regions shaded yellow! It is a powerful pattern if it agrees with future observation.
[Response: Powerful? No. It’s weak. Lame.]
“Has anyone compared Orssengo and Frank? I suspect that the only real difference is the sciencey stuff that Frank includes.”
I disagree – Frank is ideologically motivated to be dishonest (in the service of an ideological goal he believes in).
Girma’s batshit crazy.
What I did on my vacation:
Have been relearning how dedicated the effort to provide sciencey misinformation is. Under constant attack, it is tempting to think there might be something in the claims that one is seeing phantoms that aren’t there. But they are!
Girma Orssengo got a “brilliant” from RealClimate (was it Jim?) for this graph.
Susan wrote:
Yes.
In comment 106 of Handbook in Denialism, Girma wrote on 7 May 2011:
… and Jim responded:
I am just guessing, but I suspect that Jim thought Girma was being tongue in cheek, trying to create a parody of denialism. The thread was “Handbook of Denialism” and Girma ended his very first sentence with an exclamation point.
However, Girma was being serious. You can tell from a comment that received the proper reaction earlier this year. (Note the thread.) In comment 15 of The Bore Hole, Girma wrote on 9 Jan 2011:
Poe’s Law in action: Jim mistook Girma’s exclamation point meant for emphasis in the Handbook of Denialism thread as a substitute for a smiley face. Or so it would seem.
Ah, Girma Orssengo, the humble genius:
Igor Samoylenko wrote:
… then quotes Girma from 15 September 2009:
… and only 42 days later GeoCities announced that it would be closing in the United States. The good news is that a service called ReoCities has chosen to preserve much of GeoCities, even if only for historical value. Some of what it preserves includes graphics. Unfortunately they seem to have somehow missed his historic graph.
WTF? Is Girma’s cyclomania still doing the rounds?
Has anyone compared Orssengo and Frank? I suspect that the only real difference is the sciencey stuff that Frank includes.
Tamino, in your criticism of my essay on the global anomaly trend at WUWT (originally at tAV), you noted that, “It’s easy to fit a waveform to data. It’s not so easy to establish that the data are actually cyclic. … But Frank doesn’t even attempt to do so,…”
But I did do so. The first sentence of my essay said, “In my recent “New Science of Climate Change” post here on Jeff’s tAV, the cosine fits to differences among the various GISS surface air temperature anomaly data sets were intriguing.”
This was a reference to Figure 3 in the prior tAV essay, which showed the appearance of a difference sinusoid when the GISS 1999 anomalies were subtracted from the GISS 2010 anomalies. This oscillation was traced to a physical source.
I showed that this difference sinusoid arose from the inclusion, after 1999, of SSTs into the GISS global temperature anomaly data: J. Hansen, R. Ruedy, J. Glascoe, and M. Sato (1999) “GISS analysis of surface temperature change” JGR 104(D24), 30997-31022 (HRGS99). Up to 1999, the GISS global air temperature anomaly trend included only land station data.
HRGS99 also showed CRU (Land+SST) minus GISS (Land only) difference anomalies in Appendix Plate A1(b). Their difference anomalies exhibited an oscillation similar to my tAV Figure 3, but they didn’t remark on it. The oscillation shown in the HRGS99 Appendix is due to the presence of SST data in the CRU anomalies and its absence in the GISS land anomalies. My Figure 3 just extended the HRGS99 result to their own GISS data sets.
Since the oscillation appeared only after SSTs were added to the GISS global Land anomaly data set, a direct inference follows that the difference oscillation came from the SST data and reflects a global net cycle in ocean temperature that is either not present, or less present, in the land-only anomalies.
A cosine fit to the GISS 2010 minus GISS 1999 anomaly difference oscillation showed a crest-to-crest period of about 60 years.
The appearance of a difference sinusoidal period in the anomalies after inclusion of the SSTs justified looking for the parent oscillation in the global Land+SST anomaly trend. In the event, the cosine parts of the full fits to the entire GISS and CRU data sets showed about the same period as the cosine fit to the (SST+Land) minus (Land-only) difference anomalies.
So, I did show that the global air temperature anomaly trend included an oscillatory component, and I did show that it stemmed from global SST.
[Response: You’re fooling yourself, but you’re not fooling us. All you’ve done is substitute and unfounded claim of cyclic behavior in a “difference oscillation” for the unfounded claim of cyclic behavior in global temperature. You’ve gone from one claim of “It’s cyclic” with no proof, to the claim of “It includes other data which are cyclic” — again with no proof.
And there can’t be, because there aren’t enough “cycles” to show cyclic behavior. In case you don’t know (and apparently you don’t), “cyclic” doesn’t mean “it went up-and-down, then up-and-down again.” Cyclic means that it has done so often enough, and with a similar enough pattern, that we can reliably predict it will do so again.]
You wrote, “Such effort would be futile, because of the simple fact is that there aren’t nearly enough “cycles” to show that global temperature is following a cyclic pattern. Even if there were, establishing cyclic behavior is very tricky.”
If you look at Figure 3, or HRGS99 Figure A1(b), a little more than one full period of oscillation is in evidence; enough to show its presence through the 130 years prior to 2010.
[Response: It seems you’re determined to embarrass yourself, A little more than ONE full period is in evidence? You’re becoming a self-parody.
It’s also revealing that your net “evidence” consists of “If you look at …” No, you can’t just “look at” a graph and draw conclusions about cyclic behavior — especially when there aren’t enough “cycles” to show such behavior.]
Also, it’s not that, “global temperature that is following a cyclic pattern,” but rather it’s that the SSTs have apparently put a net oscillation into the global air temperature anomalies over the last 130 years or so.
[Response: Have you lost your mind? Your whole “essay” is about your model of global temperature as a linear trend plus a cycle — that’s what a cosine (or sine) is! Denying your own model, doesn’t make it look good.
But now you don’t want to call a cosine a “cyclic pattern”, you want to refer to “net oscillation”. That’s just word games. And whether it’s in global temperature, or SST, or both, you have still failed to provide any EVIDENCE other than “Looking at the graph,” and there are still nowhere near enough “cycles” to show cyclicity.]
I wrote nothing to imply anything about the fits extending to times beyond that bound, though there is presently no reason to think something like a net global SST oscillation was (or will be) not present in global average temperatures from earlier (or later) times.
[Response: SO — you admit that your whole essay is nothing but an exercise in curve-fitting?]
Concerning the fit residuals, you wrote “if you fit a linear+sinusoid model to some data, then the residuals will have zero linear slope. Necessarily. Whether the model is any good or not.”
That’s not entirely true. A fit through the unfit residual of a linear fit will have zero linear slope. The unfit residual itself can have all sorts of positive and negative excursions away from zero, including trends and oscillations. The excursions need not have a zero linear slope, but they will all average out to a zero net slope.
[Response: Mr. Frank, you are really embarrassing yourself here. You should just admit you’re wrong because you don’t know the proper use of the phrase “linear trend.” Instead, you seem to feel entitled to claim that the absence of a “zero linear slope” is compatible with a “zero net slope.”
Here’s the truth, for those who are interested: you really (really!) don’t know what you’re talking about. You’re just making up wordy phrases to justify your rather obvious incompetence.]
In my fits, the unfit residuals themselves trend along the zero line. There are no important excursions away from zero left in the unfit residuals. That’s why I showed the residuals, and what the fits to the residuals were meant to show.
[Response: Malarkey. It just “looks” that way to you for three reasons: 1) you plotted it on such a small scale that it hides the visual changes, 2) you did no statistics (anywhere), and 3) you desperately want it to be so.
I plotted *your* residuals in better fashion:
There are indeed “important excursions away from zero.” Like, the last decade.]
You wrote, “The “model” is that global temperature is following (and will follow!) a linear trend plus a sinusoid”
Your parenthetical exclamation goes too far. I made no claim that the fits predict the trend in future anomalies. I claimed only that one could find an oscillation in the anomaly trend, over 1880-2010, of a period consistent with the oscillation that appeared when SSTs were added to the land station data.
[Response: SO — once again you admit that your model is just an exercise in curve-fitting. And you continue to misuse the term “oscillation,” apparently thinking that down-and-up followed by another down-and-up justifies its use.
I can indulge in curve-fitting too. And when I did, my model came out a helluva lot better than yours.]
So you began your analysis with an incorrect surmise.
You then fitted a different data range, produced different fit parameters, and then used them to criticize my fit. I duplicated your fit. The cosine fitted over your chosen range had a period 3 years shorter, and an intensity 15% lower, than mine showed over the full 1880-2010 range. Why is it a revelation that you achieved a poorer result?
[Response: Why is it a revelation to you, that estimating parameters from most (but not all) of the data, then using that to predict the remainder, is a valid test?]
You began with a false premise (predictive model) and proceeded to a false test (improper bounds). The steep unfit residual at 2000-2010 in your second Figure only reveals the poor quality of your own extrapolation. It’s no surprise that you came to a false conclusion.
[Response: Your model utterly fails, both statistical comparison to the 4-line model, and fitting the most recent decade, even when it’s constructed using the entire time span.]
The bounds you chose [1880-1999 (end)] are not even appropriate to your premise. A proper test of my fit, granting your presumption of a predictive claim, would have required waiting for 10 years or so to see how the emerging anomalies trended. So your test was a scientific non-sequitur, apart from being an analytical malaprop.
[Response: The test I did was pretty much standard faire in what we call “science.” The bounds I chose were very favorable to you — I only required a brief “prediction” and used the vast majority of data for training the model. But you insist a predictive test would have required waiting for 10 years. And you call MY test a “non-sequitur”?]
By the way, the red line smooth in your Figure 2 evinces end-point padding, which you didn’t mention using. It helped promote that steep final gradient, though, didn’t it. End-point padding is evident in the smooths in your Figures 3, 5 and 7, as well. I consider end-point padding tendentious and never use it.
[Response: Sigh … you REALLY don’t know what you’re talking about.
There is no end-point padding. The smooth curves are a modified lowess smooth, which doesn’t use any endpoint padding.
I too dislike endpoint padding, and I never use it. But it’s a recognized (and justified) procedure (I just think there are much better ways). You’re free to avoid the practice, but clearly you are not qualified to pass judgement on it.]
I’ve already pointed out that the oscillations appeared in the anomalies after addition of the SSTs. In my essay I also pointed out, although you neglected to mention it, that the PDO and AMO include a period near 60 years, and provided a link to an article by Joe D’Aleo showing this (his Figure 11).
[Response: You’ve made it clear that you don’t really know what periodic behavior is. The AMO and PDO do *not* show periodicity. Again, there aren’t nearly enough “cycles” to show such. But you don’t seem to get this simple fact.
As for linking to Joe D’Aleo, that doesn’t help your credibility.]
Those observations together — the SST source data, the AMO and PDO periods — provided a physical meaning to the cosine part of the fit to the 130 year anomaly trend. Therefore your other tests, using arbitrarily chosen models (your Figures 3&4 and 7&8) as points of criticism, are irrelevant.
Roger Pielke Sr. has a recent guest post about work by Marcia Wyatt, Sergey Kravtsov, and Anastasios Tsonis, discussing their recent analysis of ocean thermal periods, which range around ~64 year cycles. These again allow inferring physical meaning to the cosine parts of the fits.
You wrote, “We can also compare the models using the Akaike Information Criterion, or AIC … [and] … the 4-line model wins.”
It shouldn’t have to be mentioned that statistical criteria (AIC) applied to irrelevant models do not yield any insights into the validity of a physically justified analysis.
[Response: What????????? You have lost your mind.]
At the end, your conclusion that “Frank’s model has no physical basis.” is wrong.
This comment, “It ignores the known physics of climate including greenhouse gases, sulfate aerosols (both man-made and natural), solar variations.” is an irrelevant diversion. (My analysis is an observation-based test of the claim of unusual late 20th century warming.)
And this one, “It fails the simplest test of predictive skill,…” merely turns upon your false premise.
Finally, this: “His use of results to estimate climate sensitivity is, not to put too fine a point on it, laughable.,” starting wrong and proceeding through the irrelevant, is unsurprisingly facile.
To reiterate my original point, the cosine fit was grounded in SSTs and closely corresponded to known ocean thermal cycles. Following removal of the oscillation, the remaining 130 year anomaly trend was linear to within its own noise. The rest of the analysis followed automatically, taking at face value the IPCC view of the 130 year global average surface air temperature anomaly trend.
[Response: To reiterate the truth: the cosine model does NOT have a physical basis. There is NOT established periodic behavior in AMO or PDO. To imply that they are responsible for global temperature change is idiotic.]
Pat,
In terms of data analysis (let alone the physics), the problem is you really haven’t shown anything yet. We have been down this road a few times in this forum. Check out these two posts in the archives:
https://tamino.wordpress.com/2009/12/22/cyclical-not
http://web.archive.org/web/20100104073057/https://tamino.wordpress.com/2009/12/31/cyclical-probably-not/
The second post referenced above is particularly insightful in its discussion of spectral estimation and associated techniques, problems and pitfalls.
@ PJKar
Cyclical-Not can be found (per the Archive) here:
http://web.archive.org/web/20100104072004/https://tamino.wordpress.com/2009/12/22/cyclical-not/
“There’s a shitload of bizarreness in Frank’s post: for example, after substracting the “cycles” he computes the 1880 – 1940 warming rate and then computes 1960 – 2010 rate: he then asumes that the effect of GHGs is the difference between them. Why? Because he asserts that the 1880 – 1940 rate is the rate corresponding to “LIA recovery” and GHGs effect “kicked in” around 1975!”
Not correct, Kartoffel. If you look at SPM Figure 4 of the AR4, for example, the natural + GHG-driven model ensemble output begins to noticeably deviate from that driven by natural forcings alone only after about 1950-1960. That implies the 1880-1940 temperature rise reflects primarily natural forcings, with GHG contributions slowed by the thermal inertia of the climate system.
[Response: First you said “climate of the first 40-50 years of the 20th century was unaffected by human-produced GHGs.” Now you’re backing off to “primarily natural forcings.”
By the way, the inertia of the climate system impacts all forcings, not just greenhouse gases.]
This leaves only the effect of natural forcings evident in the early 20th century global temperature anomalies. Since a rate of temperature rise by natural forcings is revealed by the early 20th century anomalies, a parsimonious interpretation of the late 20th century anomaly data is that it consists of natural plus GHG-enhanced warming. There is no obvious reason to suppose that the natural underlying rate of warming after 1950 should be different from the natural underlying rate of warming before 1950.
In an empirical analysis, one is required to be hypothetically conservative, which means using the known recent natural warming rate as the baseline beneath a recent artificially enhanced rate.
The rest of the analysis follows directly.
An empirical analysis of this sort is a test of theory. Making changes to the empirical warming rates to conform with theory injects the expected into the known. That makes the analysis tendentious.
[Response: Do you not see the fault of your argument? You’re trying to minimize the impact of early-20th-century greenhouse gases using IPCC model results. But those model results *demonstrate* exactly the consensus values of climate sensitivity that you’re attempting to dispute!
I guess you’ll accept IPCC models as evidence — unless you don’t want to.]
And we have another entry in the “can I be dumber than Pat Frank contest”:
In which our hero states: because my curve fits, you must acquit (CO2)!
I think we’ve had enough of Pat Frank’s fits.
He should see a doctor. Seizures aren’t things to be trifled with.
As another reader pointed out, if you fit a linear+sinusoid model to some data, then the residuals will have zero linear slope. Necessarily. Whether the model is any good or not.
Regression results in positive and negative residuals that have a total sum of zero. However, a linear fit to the residuals may not have a zero slope.
[Response: Wrong you are.]
A residual plot indicates whether the random errors in the model are random or independent, which is an important assumption in regression. Of course, it can also be used to identify an appropriate time series model. A random pattern of residual supports the assumption of the error randomness. The random pattern can be tested, e.g., Durbin–Watson test.
[Response: How is it that so many people who don’t know, want to tell me my business?
The Durbin-Watson test isn’t for “randomness,” it’s for *autocorrelation*. Although the lack of autocorrelation is often assumed in regression, such an assumption isn’t necessary.]
Note that a quadratic residual pattern might also yield a zero linear slope.
If the residual plot appears to have a special pattern, not necessary linear, then the model is deemed inappropriate. Then one might want to consider a different model or time series analysis.
[Response: The residual plot *does* show a pattern.]
Comparing the AICs may be a legitimate performance comparison between two models, comparing two residual plots of no big differences? Nah. You know, a higher order polynomial model usually yield better diagnostic measures, but can perform much worse in prediction.
[Response: Wrong again. Higher order polynomial models always give better R^2 values simply because they have more paramters, but the whole *point* of AIC is to compensate for the additional parameters. As for performing worse in prediction, it doesn’t get much worse than Frank’s model.]
“There is no obvious reason to suppose that the natural underlying rate of warming after 1950 should be different from the natural underlying rate of warming before 1950.”
There is no obvious reason… except for the fact that the universe doesn’t work that way. In general, absent external forcings, we would expect the climate system to tend to regress to mean. Otherwise, we’d fairly quickly (quickly, in geologic timescales) either boil or freeze the oceans.
And, in the case of early 20th century warming, we have at least _three_ explanations, only one of which also holds for the last 20th century:
1) Increasing solar TSI
2) A lull in volcanic cooling
3) Increasing GHGs
Yeah, I was going to point out that there is some data available for the early 20th century–albeit folks are still fussing over attribution for that timeframe, AFAIK.
Oh, turns out I made a hasty assumption. Pat Frank did come here to defend his WTFUWT post and… oh, I see. Waste of perfectly good popcorn, that was.
Marco | June 6, 2011 at 4:48 pm | wrote (re the similarity between the warming from 1910 to 1940 and 1970 to 2000)
Julian: “LIA recovery”. Where’s the physical mechanism?
I can suggest various mechanisms but they would be merely conjecture. Why does the planet recover from cool episodes? Random walk? I don’t know.
[edit]
[Response: That pretty well sums up the denier case.]
Pat Frank says:
If you mean “conservative” in the sense of supporting the politically-conservative point-of-view on climate change, that is certainly true. But, if you mean “conservative” in the other less-partisan sense, then what would be required would be to see how sensitive your results are to the underlying natural rate that you are just making a WAG at.
Of course, such an analysis would show that in fact your results are very sensitive to this: You can get just about any result you want with reasonable assumptions about what the natural warming or cooling rate may have been, which is why such an empirical approach, with no mechanistic understanding, really can’t get you anywhere.
The earth isn’t “telling us there’s nothing to worry about in doubled, or even quadrupled, atmospheric CO2”. Rather, your assumptions are rigging the analysis to tell you what you want to believe.
By the way, if we inhabited an alternate universe where the temperature had dropped during the first half of the 20th century, does anyone seriously believe that the Pat Frank in that universe would be arguing, “In an empirical analysis, one is required to be hypothetically conservative, which means using the known recent natural warming rate as the baseline beneath a recent artificially enhanced rate”?
I would be happy to sell that person a bridge in New York City. Rather, that Pat Frank would probably say something like, “Since naturally the temperature should go up and down about some stable value, we should assume it was going to rise back up anyway…and just look at the amount it rose in excess of what it dropped in the first half of the century as being the anthropogenic contribution.”
Recovery from little ice age was caused by roughly:
1/3rd Co2 from human emissions
1/3rd increase in solar activity
1/3rd reduction in volcanic activity
An interesting take on anthropogenic warmings other than by CO2 forcing is the blue-sky paper by Hansen: Google ‘warming in the 21st century, an alternative scenario’ for his ideas.
JF
Another gem spotted in the last post of the WTFIT (bart) : in short “it is valid to fit cosine functions on a dataset because cosine functions form a mathematical base. Therefore Frank’s analysis is correct, and then there is no CO2 effect. ”
Sure. Cosine functions form a basis of orthogonal functions, and you can project any R->R function on them nicely. Fourier basis it is called, and it’s great. Yeah.
But a basis with TWO cosine ?
And this is not even to the level of the mathturbation discussion. Projecting your data on a mathematical basis is fine and dandy, but if you have no idea of what you are physically searching for, you are doing like my PhD supervisor who spent his time jerking on his equations without making the science (of seismology) advance …
Huh.
I thought that ‘analyses’ of ‘cyclic’ time series could not get worse than those of Girma Orssengo.
Pat Frank seems determined to prove me wrong.
How is it that so many people who don’t know, want to tell me my business?
This statement is garbage. What does “no autocorrelation” mean? What does a “random pattern: mean? What does “uncorrelated error” mean? How would you interpret the test result of the Durbin Waston test? (I am not asking for your answers to these questions.)
You’ve looooked at the two residual plots of NO BIG DIFFERENCE, and consequently concluded that your model is better simply isn’t the way to go.
If I am wrong, no big deal, correct me if you can. A response of “wrong you are” doesn’t really say anything about what you know, does it?
Try the following model: x=seq(-10,10,1); y= (x+5) +0.5 *(x+5)^2 +0.5* rnorm(21, mean=0). A linear model is obviously incorrect. Find the sum of the residuals, plot the residuals and run a linear fit of the residuals against x.
In fact, try to calculate the sum of all residuals in all the statistical models you’ve run.
Show me a statistical model that the random errors are not assumed uncorrelated or independent.
An R^2 is indeed a diagnostic measure that shows a higher order polynomial model performs better. You are right, AIC does penalize for extra parameters.
p.s. I am not on anyone’s side, but simply on the side of using Statistics properly.
[Response: You embarrass yourself with this response.
In order to use statistics properly, first you have to learn how. It’s not my job to educate you, especially since it’s clear you don’t want to learn, you just want to “be right.” Good luck with that.]
With apologies to Olivia Newton John…
Let’s get cyclical
Cyclical,
I wanna get cyclical
Let’s get into cyclical
Let me here your cosine talk
Cosine talk
Let’s get orthogonal
Orthogonal
I wanna get orthogonal
Let’s get methemadical
Let me here your basis talk
Basis talk .
“Regression results in positive and negative residuals that have a total sum of zero. However, a linear fit to the residuals may not have a zero slope.”
I’ll give this a try, since Tamino has lost patience. If you read the post, you will note that Tamino specifically stated that a linear fit to the residuals WILL have a zero slope IF the regression includes a linear term. That’s because if there was a remaining slope in the residual after the fit, then the fit would be improved by adjusting the linear term to eliminate that slope.
Now, if you want to look at regressions that don’t include linear terms, then, sure, your residuals can have a slope. But that wasn’t the point of the post, which was specifically criticizing Pat Frank for developing a model that was a sine wave and a linear fit, and claiming that the lack of slope in the residuals was proof that the fit was good.
-M
Tamino,
Although the lack of autocorrelation is often assumed in regression, such an assumption isn’t necessary.
So be it if I embarrass myself! How about demonstrating this by showing me a model that such an assumption isn’t necessary?
[Response: See Lee & Lund 2004, Biometrika, vol. 91, pp 240-245.]
Yes, I do want to know if I am correct. Don’t you want to know if you are correct scholarly? Don’t you want to learn more?
M,
Regression results in positive and negative residuals that have a total sum of zero. However, a linear fit to the residuals may not have a zero slope.
This is true in general. If Tamino can give me an example to show it’s wrong, then I’ll say he knows Statistics. Patient or not, it’s his credibility on the chopping block, not mine.
[Response: You know what really pisses me off? The fact that the residuals from a least-squares regression which includes a linear term MUST have zero slope in a linear fit to the residuals, is one of the MOST BASIC RESULTS of regression theory. It’s not that complicated, it’s not at all controversial, it’s basic.
IF YOU HAD A CLUE you would already know this. But you don’t have a clue. That’s fine, most people don’t know the ins and outs of regression. But in spite of your astounding ignorance, you have the unmitigated gall to try to lecture me about regression and to suggest that *my* credibility, not yours, is on the chopping block. It’s not your ignorance that’s offensive, it’s the extreme level of arrogance which is almost unbelievable.
We agree on one thing: your credibility is not on the chopping block — because you don’t have any.]
JH, I think this answers all your questions.
Don’t be downhearted. If you actually learn some statistics, you will be able to look back on the nonsense you spewed and laugh at your mistakes.
You know, I occasionally suffer from D-K but I tend to avoid letting it hang out in all it’s glory on a public venue.
I must embarrass easily.
The fact that the residuals from a least-squares regression which includes a linear term MUST have zero slope in a linear fit to the residuals, is one of the MOST BASIC RESULTS of regression theory.
The fact? A least-squares regression? Any least square regression? Yes, you are only correct IF the data strictly follow a linear model. “Including a linear term” means there can be other terms, e.g., quadratic term, in the systematic part of the model.
[edit]
[Response: You are way over the line arrogance-wise, and way beyond the “stupid threshold.” B-bye.]
Dude, think about it. If there is a linear term, a linear fit will match it. Anything left over, the residuals by definition, is NOT linear. It ain’t that tough.
Tamino: you really need to have an equivalent of RC’s Bore Hole or similar places elsewhere, and (everybody) bug WordPress to make the tools better to this gets trivial.
Given “Open Mind”, maybe a good title for it would be “So open, brains fell out”.
In my experience, I have not yet seen anyone deep into Dunning-Kruger ever recover.
JH
You have a function
sampled at a collection of points 
.
by a function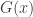 
in some class of functions 
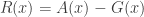and you want 
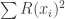minimal over all choices of 
.
You want to approximate
(closed under addition) with minimal squared error. So set
If you now do the same thing with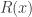
that you did with 
, then the approximation function 
for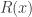 
must be 
because otherwise
but
so 
does a better job approximating the function 
than 
did. Contradiction.
This should be consider a prove that JH is brain dead.
I was on the way to do once again this demonstration with the same path (demonstrating that the result is false with an absurd hypothesis), but you did it better than I would have done quickly.
Of course, I could rewrite that totally formally with epsilons and things like that, but you said everything. Thanks
“The fact? A least-squares regression? Any least square regression? Yes, you are only correct IF the data strictly follow a linear model. “Including a linear term” means there can be other terms, e.g., quadratic term, in the systematic part of the model.”
Try it. Open up your favorite stats program – heck, even Excel. In one column, place the numbers 1, 2, 3, 4, … In the second column, place the numbers 1, 4, 9, 16, … Do a LINEST regression. Then, using the intercept and slope provided by LINEST, calculate a new set of numbers. Take the difference between the new set and the original quadratic. Do a second LINEST of that difference (eg, the residual). Voila! Zero slope!
If you have a linear term in your regression model, then there will be NO linear slope in the residuals, BY DEFINITION. The fit might suck (see the above example of making a linear fit to a quadratic formula), but the slope in the residuals is zero. This is, as has been pointed out to you several times, a very basic fact that _should_ be understandable to anyone with a basic grasp of what a regression implies, if they are willing to THINK about it for more than 3 seconds.
Just for laughs, I did just that. Me not having much stats background & all, I didn’t previously know that a linear fit leads to a zero slope on the residuals, though it certainly makes sense when I think about it (but stats being stats, that’s not always a good test!)
I did up a table of the equation y = 24 x^3 – 56 x^2 + 224 x + 6 (coefficients chosen randomly).
Ran a linear regression in Excel (yes, the fit was bad!). Took the residuals, ran another regression.
The slope of the linear fit to the residuals was -0.000000000000134832.
See, it wasn’t zero, JH was right! :-P
The error bar is pretty huge: 95% bounds are -1000.48896 & 1000.48896
Does anyone remember what precision Excel uses? I know I’ve bumped up against it a couple of times with my work, which generally doesn’t concern particularly large (or small!) numbers, so it’s not fantastic by any stretch of the imagination…
This looks like a pretty obvious example of floating point rounding error. I ran into this recent when working with a database. I had stupidly defined a column (which should have been of type ‘money’ as ‘float’. Storing a rounded exact value (x.xx) in this field resulted in a value of x.yyyyyyyyyyyyyyyyy which when rounded was x.xx. Changing the column to ‘money’ fixed the problem.
Your value, for all practical purposes, is zero. It is just a representational issue.
Hmmm but you shouldn’t do a linear regression, but a regression including a linear term (among others).
Sorry, I should have added the [sarcasm] tags to that line after the slope… looking back on it, I may have been a bit too subtle. :-D
Yes, I’m well aware it’s a rounding issue, resulting from the limitations of Excel’s numerical precision. 1.3e-13 is a pretty small number, by any stretch of the imagination, and I suspect Excel’s (reliable) error margin is probably approaching 1e-12, or something like that.
double-precision IEEE standard floating point yields 15 digits, and this is what Excel implements (it’s due to the fact that underlying hardware from Intel and others implement the standard).
But computation can lessen the number of significant digits (pathologically, down to zero) so as RN has said, you’re a victim of the fact that floating point arithmetic is imprecise. You can actually get better looking results in binary (log2(10) has no rational representation therefore naively converting binary floating point to decimal floating point can lead to a lot of weird digits on the right that won’t be there in the original binary representation) but floating point arithmetic is imprecise at heart, regardless of separate issues regarding converting binary to decimal.
# The following script will provided endless hours of fun illustrating this point.
rm(list = ls())
# Generate some data.
n <- 10
x <- 1:n
y <- log(x) + (1/x) # Put whatever function you want here.
# Regress y against x. Get the predicted values.
reg.xy <- lm(y ~ x)
f.y <- predict(reg.xy)
# Get the residuals.
e <- residuals(reg.xy)
# Regress the residuals against x. Get the predicted values.
reg.xe <- lm(e ~ x)
f.e <- predict(reg.xe)
# Plot the data.
par(mfrow=c(1,2))
# Plot y vs. x and its regression line.
plot(x, y, ylim = range(c(y, f.y)), main = 'y vs. x', type = 'b')
lines(x, f.y, lty = 2)
# Plot the residuals vs. x and its regression line.
plot(x, e, ylim = range(c(e, f.e)), main = 'e vs. x', type = 'b')
lines(x, f.e, lty = 2)
# Print the regressions' summary statistics.
summary(reg.xy)
summary(reg.xe)
Horatio just has one question (or maybe two):
If Horatio removes the cheese from a mouse trap (without getting caught, of course) does that mean the cheese is completely gone?
Or is there perhaps a way of getting more cheese from the same trap?
Off topic, but over at Deepclimate it appears that the hypothesis that at least some traps yield unlimited amounts of cheese … or … plagiarism if you prefer … is being shown to be true.
(more wegman stuff)
Tamino and many commenters may be interested to note that they are apparently much smarter than a Cambridge professor:
http://www.climateconversation.wordshine.co.nz/2011/06/prof-kelly-shows-the-middle-way/
I am not surprised, I must admit. Someone who actually takes something from WUWT and considers it a valid starting point has lost all ability for critical thinking.
Not only WUWT, but CA also! The words “engineering-standard” analysis are a real tip off there. BTW, wasn’t this guy on the Oxburgh or Muir-Russell comission?
It is worse than that.
In that piece, not only does he refer in all seriousness to the “analysis” by Frank (which as Tamino showed here is nothing more than glorified numerology), but also he actually manages to misinterpret it! He says Frank’s article “… concludes that it is rising temperatures that are increasing the atmospheric carbon dioxide, not the other way round.”
WTF? Professor, FRS, FREng – my arse!
OMG. If Frank’s analysis is “engineering-standard” I’m never plugging in another device or getting on another moving vehicle in my life, he wrote, edging quietly back from his laptop…
That’s depressing beyond words. If an FRS can’t see through the curve fitting nonsense, what chance do we have with anyone else?
Nine months ago Kelly was part of the group that produced and endorsed the Royal Society’s “Climate change: a summary of the science”: http://royalsociety.org/climate-change-summary-of-science/
I am very disturbed that he now feels Pat Frank’s analysis is capable of overturning this document’s conclusions.
From the comments, it’s a colony of WUWT.
Prof Kelly: “This concludes that it is rising temperatures that are increasing the atmospheric carbon dioxide, not the other way round. ”
What? Really? I realize that maybe this sounds good to the ignorant, but it amazes me every time that a supposedly “high-caliber” skeptic (eg, those with PhDs and Professorships) trots this one out… I can understand “climate sensitivity is low”, but “the increase in atmospheric concentrations is due to temperature”? Really?
M, I’ve seen that argument a few times. A well known shock-jock here in Australia recently trotted it out when ‘interviewing’ (interrogating was more like it!) a climate scientist. He claimed that because the oceans were 70% of the earth’s surface, they were more likely to be the cause of increased CO2 than humans. He blissfully ignored the response from the climate scientist that the opposite was true, that the oceans were *absorbing* half the CO2 we emitted.
I thought CO2 was supposed to follow warming with an 800 year lag?
@John Brookes, the laymanexplanation: The 800 year lag is still probably largely true, except since Humans have been pumping in amongst billions upon billions of tonnes into the atmosphere decade after decade and rising [in 2010 we broke the 2008 the output record by 5%], we’ve pushed that cycle way ahead. As most know, you too I’m sure, CO2 at it’s peak in that cycle elevates temps [it’s a GHG after all] and slows the cooling into the next ice-age, a padding effect for a softish landing. Humans having now increased it from the normal peak at ~300 ppmv WAY AHEAD of time from 280 to 394 ppmv and rising, have undertaken to amplify the warming signal greatly.
–//–
It does rather test Emerson’s dictum that “consistency is the hobgoblin of small minds,” doesn’t it?
Oh, wait, it’s coming back to me that the full description is “a foolish consistency. . .”
I suppose that given enough foolishness, inconsistency and consistency can coexist in a small, tortured mind.
I have seen changes in the figures depending upon the study. May be as short as 100-200 years. But the relationship between carbon dioxide and temperature is reciprocal. Temperature may rise first or carbon dioxide may rise first. Raise the temperature and you reduce the ocean’s capacity to hold carbon dioxide and therefore it releases some the carbon dioxide it already has.
Raise the level of carbon dioxide and your reduce the rate at which thermal radiation is able to escape the top of the atmosphere. Assuming energy continues to enter the climate system at the same rate the amount of energy in the system will slowly rise until the rate at which thermal radiation is emitted compensates for the increased opacity of the atmosphere to thermal radiation.
Both of these feedbacks follow from fairly basic physics. And as a matter of fact, we were studying the role of carbon dioxide in the greenhouse effect back in the mid-1800s and before. You can see it in satellite images such as those taken by the Atmospheric InfraRed Sounder aboard the Aqua satellite. You can demonstrate the absorption of thermal radiation in a classroom. We know the basis for carbon dioxide’s ability to absorb thermal radiation in the atmosphere in terms of it bending mode of molecular excitation. We are able to identify its absorption spectra due to this mode of excitation. We are able to measure its effects upon the transmission of radiation through the Earth’s atmosphere.
And we know that there have been times in the Earth’s history when carbon dioxide rose first. And those times that carbon dioxide rose first are strongly associated with sudden changes in climate and the resulting major and minor extinction events.
For example:
55 Mya, Paleocene-Eocene Thermal Maximum – North Atlantic Basalts
65 Mya, end-Cretaceous event resulting from a supervolcano that gave rise to the Deccan basalts in India as it collided with Asia at the time of the formation of the Himalayas
183 Mya, Toracian Turnover (a lesser warming and extinction event in the Early Jurassic period) – Karoo Basalts (Africa)
201 Mya, End Triassic Extinction – Central Atlantic Magmatic Province
251 Mya, Permian-Triassic Extinction that resulted from a supervolcano that left behind the Siberian basalts during the breakup of Pangaea.
360-375 Mya, Late Devonian Extinction – Viluy Traps (Eastern Siberia, more tentative according to Rampino below)
For a more extensive list, please see:
Vincent E. Courtillot and Paul R. Renne (2003) On the ages of flood basalt events, C. R. Geoscience 335, 113–140
http://www.mantleplumes.org/WebDocuments/CourtRenne2003.pdf
For a recent commentary:
Michael R. Rampino (April 13, 2010) Mass extinctions of life and catastrophic flood basalt volcanism, PNAS, vol. 107, no. 15, pp. 6555-6556
http://www.pnas.org/content/107/15/6555.full
Here is recent study showing that the eruption of the Central Atlantic Magmatic Province occured simultaneously with the end Triassic Extinction 201 Mya:
Jessica H. Whiteside (April 13, 2010) Compound-specific carbon isotopes from Earth’s largest flood basalt eruptions directly linked to the end-Triassic mass extinction, PNAS, vol. 107, no. 15, pp 6721-6725
http://www.pnas.org/content/107/15/6721.full
One resource well worth mentioning is:
Large Igneous Provinces Commission
International Association of Volcanology and Chemistry of the Earth’s Interior
http://www.largeigneousprovinces.org
… and here is a blog that may also be of interest that focuses oftentimes on the intersection of climatology and geology:
olelog – What on earth
http://my.opera.com/nielsol/blog
I believe it is worthwhile to mention these events in deep geologic time anytime someone raises argument that “temperature always rose first.” It didn’t. In some cases carbon dioxide rose first, then temperature. However, I should also note that these eruptions are on a far greater scale than anything we have seen in the past few million years and are typically associated with the breakup and formation of continents or the formation of ocean plateaus. The Siberian Traps associated with the End Permian Extinction of 251 million years ago (MYA) has a volume of 1.6 million cubic kilometers. The smallest LIP listed is the Columbia River Flood Basalts and it appears to be associated with the End Early Miocene 16 MYA. The volume of that structure is roughly 170,000 cubic kilometers.
In contrast the the ejecta from the explosive eruption of Mt. St. Helens had a volume of one cubic kilometer, Pinatubo ten cubic kilometers, and the Yellowstone Caldera of 600,000 years ago, roughly 1000 cubic kilometers or 100 Pinatubos going off simultaneously — leaving an ash bed covering roughly half of the area of the 48 contiguous states of the United States is less than 1/100th of the Columbia River Flood Basalt eruption of 16 Mya.
Timothy wrote: “I believe it is worthwhile to mention these events in deep geologic time anytime someone raises argument that “temperature always rose first.”
I do, often. It’s almost always met with a blank stare, or an awkward change to another stock talking point.
Please note that Roy Spencer once tried the same argument. Using some wondrous mathturbation, he ‘showed’ that 80% of the increase in CO2 in the atmosphere was due to outgassing from the ocean.
http://www.drroyspencer.com/2009/05/global-warming-causing-carbon-dioxide-increases-a-simple-model/
Note his attempt at making *any* objection to his model into a political attack (“see, I’m right”).
Seems someone (Spencer), doesn’t even realise he lacks an ENORMOUS sink if increasing CO2 is mainly due to ocean warming. A sink that takes up 5 times more than mainstream science has the oceans take up. Guess the biosphere has increased with several hundreds of gigatonnes the last few decades…(I wonder where it all went)
[Response: Don’t forget this.]
WUWT is a “least neurons regression”.
A few years ago, i about 0.5% of members the American Physical Society, mostly physicists with PhDs, signedpetition that effectively required ignoring basic physics.
I did an analysis of the demographics, which was heavily skewed older than the membership as a whole, skewed conservative to the extent there was evidence, and likely skewed male, although that wasn’t statistically significant, as there aren’t enough older female physicists. Anyway, 6 months of noisemaking and hard campaigning got ~200 signatures.
Most PhDs do *not* “go emeritus” in the bad way, in fact, some do some absolutely terrific work after they “retire”, like Burt Richter, whose idea of retirement would exhaust most people.
John M, Greenfyres has a nice graphic here.
M: “I realize that maybe this sounds good to the ignorant, but it amazes me every time that a supposedly “high-caliber” skeptic (eg, those with PhDs and Professorships) trots this one out…”
There is such a thing as stupidity sent to college.
You would have to be an idiot to draw the conclusion Kelly does from Frank’s essay and you would also have to ignore to the point of dishonesty all the evidence pointing to the oceans and biosphere being net absorbers of CO2. Kelly is a denier, not a sceptic. For more of his views, see his Input for the CRU Review. (The PDF also contains “evidence” from Holland, Keenan, and Montford.)
Anyone interested in science can only feel utter revulsion at Franks article. What kind of fool first trashes the data with something like this:
“It seems certain that surface air temperatures are so contaminated with systematic error – at least (+/-)0.5 C — that the global air temperature anomaly trends have no climatological meaning.”
And then with the same data and anomalies (to paraphrase: lets assume the data is OK just for this demonstration) he goes on to perform computations of warming rates, periodicities and amplitudes of various phenomena he claims exists, changes in warming rates and climate sensitivities all with apparent zero error.
What a pathetic fraud.
Interestingly Tisdale called him on the AMO + PDO oscillation. From Tisdale’s comment: “As discussed on the thread of tAV cross post, this post (Franks post-pjkar) would have been better without the reference to the meaningless PDO+AMO dataset.”
The meaningless PDO+AMO dataset. That would appear to be a more or less complete trashing of Franks the “secret is in the cosines” takeaway message wouldn’t it?
We can only hope that this circus of the absurd will somehow extinguish itself but I can’t help but feel the opposite will happen.
Yes, classic deniotripe: the data are rubbish or a simple fraud unless I can use them to “prove” that AGW is rubbish or a simple fraud. This won’t stop. They can’t help it. It’s part of their makeup.
Tim, thanks for the detailed info on CO2 excursions. Interesting stuff.
Thank you, Barton.
I have heard that the best precedent for what is taking place today is the Paleocene Eocene Thermal Maximum, but I suspect it would be easy to carry this too far.
One of the great things about the supervolcanoes: they knew how to clean up after themselves. All the exposed flood basalt at the surface or along the ocean floor helped bring down atmospheric concentrations of carbon dioxide through weathering, mineralizing it, accelerating the rate at which carbon was returned to the deepest of carbon pools in the carbon cycle.
I somewhat doubt that the current supervolcano will be quite so tidy. But higher temperatures will also mean the acceleration of the hydrological cycle, increased droughts and flash floods, the blowing and washing away of topsoil and exposure of rock. These things always seem to have a way of working themselves out. Sometimes it just takes longer.
However, some of the more recent work that may be of interest are the so-called “hyperthermals” where methane was released episodically during the Paleocene Eocene Thermal Maximum. I won’t try to summarize it at this point except to say that there were evidently more of these than we had previously thought, and since they involved the transport of carbon from shallower carbon pools the recovery time was much shorter.
Not that this would have mattered much to the poor animals at the time of the excursions themselves.
I personally prefer to look at the relationship between mean global surface temperature and atmospheric CO2 abundance — these are the variables that you expect to be correlated on theoretical grounds. Otherwise you’re trying to correlate two quantities that are imperfectly related, since CO2 hasn’t increased consistently year by year (especially in the earlier part of the 20th century). Here is the dT-CO2 figure, showing annual means based on GISS data:
This regression line captures most of the information content in the dT-CO2 at least on timescales longer than a few years. This simple linear fit is quite good, with a Pearson correlation coefficent of R=0.91. The slope of the linear trend is 0.00087 C/(ppm CO2) or 2.35C per doubled CO2 (from 270 ppm). The standard deviation is 0.11 C. In this 130-yr dataset, only 3 points exceed 2 s.d., and none exceed 3 s.d. (the largest deviation is +2.87 sigma in 1944).
Trying to add an additional sinusoid component does not seem justified. Much of the variability seen in the T vs. time plot is missing from the T vs. CO2 figure. This suggests that much of the irregular residuals (after linear detrending of the T-yr plot) stems from variable rates of fossil fuel burning in the early part of the 20th century (especially during the Great Depression). However, it is evident that there is a cool period from about 1900-1920, a warm period from 1930-1950, and a slight cooling through the 1960s (which confirms these well-known temperature anomalies).
As others have noted, taking noisy data and fitting it to some chosen function is of limited utility. How does one choose the function to fit? There has to be some physical reason for the choice. Linear plus sinusoid? Why? This is the kind of thing a physicist does in the privacy of his own office. If he discovers that the period of the sine wave matches some other known period (like insolation for example), then he can proceed to an hypothesis and test such against the data. If the period doesn’t match anything else, then he has NOTHING. As Tamino points out, a linear slope (slope plus intercept) plus a sinusoid (amplitude plus phase) comprises 4 parameters. As my thesis supervisor liked to say: Give me 4 parameters and I’ll fit an elephant. And Frank finds the period to be 60 years. That’s pretty weak for a sinusoid fit; just 2 periods over all the data? Get serious. And what is it that’s fluctuating with this period? Nothing? Then Frank, you’ve made ZERO contribution to the field. Sorry, that’s the way science works. Next idea?
But we do have a perfectly good theory on what’s happening. Extra CO2 in the atmosphere traps some heat: the physics has been known for over 100 years. Can we calculate how much? Yes we can calculate the primary effect, but the feedbacks are extremely difficult to calculate. Do the models with feedbacks; include albedo, water vapor, etc. Result is a climate sensitivity of about 2 degrees for a CO2 doubling. Now the test: plot global temperature against CO2 concentration as Phil has done (brilliant idea!). Result: a linear fit (2 parameters only) 2.35 degrees per doubling. Now we have something; agreement with theory. That’s how science is done!
Frank: Pick up your marbles and go home.
Rick A. Baartman …
Thank you for stating the obvious so eloquently ….
(I mean this in a very positive way, well said!)
Rick, if you actually read my posts you’ll have seen that the ~60 year sinusoid showed up in the anomaly trend when the marine temperatures were added to the land-only temperatures. That implies a physical cause; your objection has no basis.
[Response: No, it doesn’t; the suggestion is ludicrous.]
Atmospheric CO2, by the way, traps energy not heat. How the climate works determines whether that energy appears as sensible heat. Your analysis is careless.
[Response: Keep digging that hole.]
This response is rather long, and so I’ve posted it in three parts.
Tamino: I wrote, “So, I did show that the global air temperature anomaly trend included an oscillatory component, and I did show that it stemmed from global SST.”
You wrote in response: “You’re fooling yourself, but you’re not fooling us. All you’ve done is substitute and unfounded claim of cyclic behavior in a “difference oscillation” for the unfounded claim of cyclic behavior in global temperature…“
Unfounded claim? Readers are invited to look at Figure 3 here. The difference oscillation shows nearly two full periods. It appears in the GISS difference data only after the ocean temperatures were added in. That’s a demonstration, which is rather different from an unfounded claim. Who should we believe, Tamino: you, or our lying eyes?
[Response: Like most mathturbators, the sum total of your “evidence” consists of “look at.”]
You then wrote, “You’ve gone from one claim of “It’s cyclic” with no proof, to the claim of “It includes other data which are cyclic” — again with no proof.”
The sentence “It includes other data which are cyclic” appears nowhere in my essay. Why did you put it in quotes as though I wrote it?
The logic is very straightforward. An oscillation appears in the global air temperature difference anomalies only after the marine temperatures are added to the land air temperatures. That must mean an oscillation entered with the marine data. One is then led to look for the oscillation in the full data set. There’s nothing mysterious here.
You wrote: “And there can’t be, because there aren’t enough “cycles” to show cyclic behavior.”
Curious: there are two cycles showing cyclic behavior.
You wrote: “In case you don’t know … Cyclic means that it has done so often enough, and with a similar enough pattern, that we can reliably predict it will do so again.”
Not correct. A statement about cycles in some data implies nothing about future events. It implies something about the data. You are making an unwarranted inferential extension. Stating the data set ‘shows cyclic behavior’ means that cycles are observed in the data under examination. It says nothing about whether those particular cycles are extensive.
One can hypothesize that the cyclic behavior will continue. Whether cycles are observed in future data tests a hypothesis about the future. But none of that impacts whether cycles are observed in the data we have now. And when we look, there it is in Figure 3.
You wrote: “It seems you’re determined to embarrass yourself, A little more than ONE full period is in evidence? You’re becoming a self-parody.”
Admitted, I misstated the case. There are nearly 2 full periods in evidence.
You wrote: “It’s also revealing that your net “evidence” consists of “If you look at …””
Figure 3 shows a cosine fit. The evidence is that a cosine fit goes right through the middle of oscillatory difference anomalies. Your criticism is a careless misrepresentation.
You wrote: “No, you can’t just “look at” a graph and draw conclusions about cyclic behavior”
Isn’t that what you’re doing with your dismissal by visual judgment?
“— especially when there aren’t enough “cycles” to show such behavior.”
Almost two full cycles plus a good fit with a cosine function are enough to show that an oscillation is present.
In response to your original criticism, I wrote that, “Also, it’s not that, “global temperature that is following a cyclic pattern,” but rather it’s that the SSTs have apparently put a net oscillation into the global air temperature anomalies over the last 130 years or so.”
Your reply: “Have you lost your mind? Your whole “essay” is about your model of global temperature as a linear trend plus a cycle — that’s what a cosine (or sine) is! Denying your own model, doesn’t make it look good.”
You have now shifted the ground of your argument. You initially wrote about “global temperature following a cyclic pattern.” Those weren’t my words, and that idea does not appear in my analysis.
My analysis found a ~60-year cosine-like oscillation within the 130-year global air temperature anomaly trend. There’s nothing in that about the global trend itself following a cyclic pattern. Your original description was incorrect, and your current description of the model as “a linear trend plus a cycle” itself contradicts your original “cyclic pattern” description.
You wrote: “But now you don’t want to call a cosine a “cyclic pattern”, you want to refer to “net oscillation”. That’s just word games.”
No. “Net oscillation” refers to the fact that the oscillation initially showed up in a difference anomaly data set. I.e,. it’s what emerges after the two data sets have been differenced. This isn’t as hard as you’re making it.
You wrote: “And whether it’s in global temperature, or SST, or both, you have still failed to provide any EVIDENCE other than “Looking at the graph,””
Well, except for the nearly two periods that show up in the difference anomalies, except for the cosine fit to the difference anomalies, and except for the two cosine + linear fits to two methodologically independent anomaly data sets. And, except for the fact that those two independently fitted cosines may as well be of the same frequency and phase. Except for all that, no evidence.
“and there are still nowhere near enough “cycles” to show cyclicity.”
Nearly two periods in evidence plus a good cosine fit are enough to show cyclicity, but only if one examines the data itself without an artificial, unwarranted, and imposed condition that cyclicity observed now is not present now unless one has miraculous pre-knowledge of future nows.
After I explained to you that, “I wrote nothing to imply anything about the fits extending to times beyond that [130-year] bound…”
You responded: “SO — you admit that your whole essay is nothing but an exercise in curve-fitting”
You’ve made yet another untoward inference. My analysis was an exercise in physical phenomenology. That’s when one takes real physical data (temperature anomalies) and, within a physical context (global thermal behavior), uses physical reasoning to examine the data in terms of mathematical functions that reflect common natural phenomena (cycles).
As I noted above, one could extend the model as an empirical conjecture and suggest that if the thermal oscillation found in the global air temperature anomalies reflected a global net effect of on-going energy flux in the oceans, then one should observe it in the future trend of air temperature anomalies. At that point, one sits back and waits for the data to come in. Conjecture, test, refutation/verification — the method of science.
You wrote, “you seem to feel entitled to claim that the absence of a “zero linear slope” is compatible with a “zero net slope.”
You continue to infer what is not in evidence. You claimed that the residuals of any linear fit “will have zero linear slope. Necessarily.“ I replied that is not entirely true, pointing out that the residual of a linear fit can have arbitrarily large excursions from linearity, but will always average out to zero trend. The zero average produces a fit with zero slope, even though the fit residual may excurse up, down, and all around.
Your explanation was sloppy and misleading; zero net slope is descriptively much closer than “zero linear slope” to the generalization of the sort of residual one can get from a linear fit.
Further: the context of my comment was the linearity of the Figure 1 fit residuals themselves. I.e., Figure 1 Legend: “The colored lines along the zero axis are linear fits to the respective residual. These show the unfit residuals have no net trend.”
The zero slope of the residuals, not of the fits to the residuals, shows that all of the signal is accounted for in the cosine+linear fits. The zero slope fits to the zero slope residuals just visually emphasizes this fact. No significant excursions. This is not very hard to understand.
At this point in your response, you wrote: “Here’s the truth, for those who are interested: you really (really!) don’t know what you’re talking about. You’re just making up wordy phrases to justify your rather obvious incompetence.”
Thank-you for that: it provides me an opportunity to summarize your argument thus far. You’ve dismissed the empirical demonstration of an oscillation in observational data on the grounds of needing a miraculous prescience of future cyclicity. In so doing, you displayed an apparent non-recognition of standard phenomenological analysis. You’ve improperly inferred meaning where it did not exist, and missed meaning where it was presented. Your argument has thus far rested upon continued misconstrual and thereafter you proposed that I’m incompetent. Good job.
[Response: It’s not worth my time to argue with an idiot. If readers want to do so, that’s their choice.]
Part 2:
Tamino, you wrote: “Malarkey. It just “looks” that way to you for three reasons: 1) you plotted it on such a small scale that it hides the visual changes, 2) you did no statistics (anywhere), and 3) you desperately want it to be so.”
I overlooked putting a scale on the residuals plots, it’s true. Apologies. That was an oversight. The scale was 0.2 C per division. But in any case, comparative inspection of the noise readily shows that the residuals and the anomalies were plotted on a similar scale. That takes care of the substance of your “1).” Your “1)” also improperly implies a motive not in evidence. So does your “3).” For your “2),” the statistics of these fits are less important than showing the uniformly zero-slope of the residuals, which demonstrate that the fits account for the great majority of the anomaly signal.
You wrote: “I plotted *your* residuals in better fashion: … There are indeed “important excursions away from zero.” Like, the last decade.”
How about the residual for 1890-1900 and 1940-1950? Those decades show excursions just as large as the last decade, except they’re not conveniently at an end-point. How did you miss realizing that? They show the residual is noisy throughout, vitiating your entire point.
In fact, if our audience squints at your smoothed line, they’ll see what looks like a weak cycle traversing the residual, which you’d say isn’t there because we have no miraculous prescience about its future extension. A cosine fit the GISS or CRU residual does indicate a weak oscillation in each of them, about twice as intense in the CRU residual [~(+/-)0.09 C) as in the GISS residual [~(+/-)0.45 C). But, neither really emerges from the noise, so one shouldn’t make too much of them.
You wrote: “SO — once again you admit that your model is just an exercise in curve-fitting.“
As already noted the last time you supposed this, you’ve inferred what was not in evidence, and have apparently not recognized a straight-forward phenomenological analysis.
“And you continue to misuse the term “oscillation,” apparently thinking that down-and-up followed by another down-and-up justifies its use.”
Two cycles are two cycles. This simple fact escapes your gaze, fixated as it is, apparently, on needing to foresee the future so as to recognize what is in plain sight today.
“I can indulge in curve-fitting too. And when I did, my model came out a helluva lot better than yours.”
None of your models except the first one are justified by a signal that emerged after one variable was changed in one of two otherwise homologous physical data sets. That makes them irrelevant.
In response to the point that you fit your sinusoidal test model over a different data range, you wrote: “Why is it a revelation to you, that estimating parameters from most (but not all) of the data, then using that to predict the remainder, is a valid test?”
Fine, then let’s put the models to a valid climate-science style test of goodness. I duplicated your 1880-1999 cosine+linear test fit as: anomaly T = -0.0871*cos(6.581*YYYY)+0.00502*YYYY-9.817, where YYYY=4-digit year.
Then in proper climate science fashion I regressed it against the entire 1880-2009 data set. The correlation r^2 was 0.833 (p lt 0.0001); pretty darn good, even for climate science.
The same regression of the full 1880-2009 cosine+linear fit over the same entire data set: anomaly T = -0.103*cos(6.575*YYYY)+0.00575*YYYY-11.21, showed only a slightly improved correlation r^2 of 0.844 (p lt 0.0001). So, your more limited fit is hardly worse than the full fit.
Further, if one regresses the 2000-2009 residuals obtained by extrapolating your 1880-2000 fit, against the 2000-2009 residuals obtained from the full 1880-2009 fit, the correlation r^2=0.97 and the mean difference of the residuals is 0.1 C; equivalent to the noise of the unfit residual [(+/-)0.1 C, 1880-2009; (+/-)0.09 C, 1880-1999]. For anyone interested, that means they’re the same to within about 1-sigma.
But we can go even farther. One should detrend these data sets when specifically looking for a periodic signal. So, I did that by separately fitting lines to the full GISS 1880-2009 and to the truncated GISS 1880-1999 data sets, and then subtracting its fitted line from each set over its entire range.
I then looked for an oscillation in the detrended 1880-1999 data, i.e., your truncated test data, and in the detrended 1880-2009 data, i.e., the full data set, using the same cosine function as before, a*cos(b*YYYY), where YYYY is again the 4-digit year.
The result:
1880-1999: -0.054*cos(5.01*YYYY); (detrending slope: 0.049 C/decade)
1880-2009: -0.060*cos(5.01*YYYY); (detrending slope: 0.057 C/decade)
That is, both time regions yielded fitted cosines with virtually identical phases and periods, but with slightly different (0.9:1) amplitudes.
A look at the two detrending slopes reveals the major cause of the poorer quality fit of your chosen test range. Removing the end-point warm years of 2000-2009 down-tilted the linear part of your fit. The problem of a poorer fit does not reside in the cosine part.
We can notice this as well when looking at the coefficients of the above cosine+line fits over 1880-2009 and 1880-1999: the cosine periods are identical to within 0.01, but the slopes of the linear parts differ.
So, both data sets support the same oscillation and are within 0.1 C of the observed trend over the prediction range of 2000-2009. Indeed, the standard deviation of the 2000-2009 residuals from your truncated fit range is (+/-)0.09 C, relative to (+/-)0.08 C for the residuals of the full range fit, no matter the steep 2000-2009 residual line you chose to emphasize.
So, at the end, the cosine+linear model easily passes your truncated data set verification test.
Part 3:
Continuing: after I pointed out that you composed your original criticism with the false premise of a predictive model, you wrote: “Your model utterly fails, both statistical comparison to the 4-line model, and fitting the most recent decade, even when it’s constructed using the entire time span.”
Your 4-line model stems from no physical inference and is irrelevant. To the contrary, the cosine+linear model does so stem and is therefore phenomenologically relevant. The model is now shown to succeed both over the full data range and over your own chosen truncated range.
Both produce the same underlying oscillation, which can then legitimately be subtracted from the full anomaly data set to yield the net linear 130-year warming trend. My original analysis is again justified and follows directly.
You wrote< “The test I did was pretty much standard faire in what we call “science.””
It’s standard fare in proxy reconstructions of paleo temperatures. We can agree to disagree about whether that field is science. So, I’m glad you chose to enquote the word. However, typical in science is to predict the appearance of results not yet in hand; results to be obtained by further experiment or observation. In any case, as we’ve all now seen, the cosine+linear model passed your chosen test to high climate-science verification standards.
When I suggested you used end-point padding in your smooth, you wrote: “Sigh … you REALLY don’t know what you’re talking about.” and indicated having used a Lowess smooth. Great. We’re all relieved. But you didn’t mention your method in the original critique.
Given the widespread use of end-point padding in climate science, my inference is hardly surprising or extreme. So, your mannered sigh and pointed comment appear to be the opportunistic exploitation of an understandably mistaken inference stemming from your own methodological silence.
After I mentioned the analogous periodicity of the AMO and PDO, you wrote, “You’ve made it clear that you don’t really know what periodic behavior is.” By now everyone knows that recognition of cyclicity is empirical, and that your criterion of cyclicity by prescience is nonsense.
You then wrote, “The AMO and PDO do *not* show periodicity. Again, there aren’t nearly enough “cycles” to show such. But you don’t seem to get this simple fact.”
Maybe you should read Marcia Wyatt?s comment here and the comments following, and take a look at the fact of this plot, obtained from the same comment thread.
Your disparagement of Joe D?Aleo is unworthy of reply.
When I mentioned that, “statistical criteria (AIC) applied to irrelevant models do not yield any insights into the validity of a physically justified analysis,” you replied, “What????????? You have lost your mind.”
So, as you clearly disagree, suppose you explain how statistical criteria applied to irrelevant models yield positive insights into the validity of a physically justified analysis. That should be fun.
And, finish line thankfully in sight, we reach your final words: “To reiterate the truth: the cosine model does NOT have a physical basis.”
Demonstrated wrong.
“There is NOT established periodic behavior in AMO or PDO.”
Demonstrated wrong.
“To imply that they are responsible for global temperature change is idiotic.”
Obviously irrelevant: I never wrote or implied they are so responsible.
To reiterate what I actually did write with respect to the PDO+AMO: they display about the same ~60 year periodicity as the fitted oscillation in the 130-year global air temperature anomaly trend. They were offered as a surrogate for a net global ocean thermal cycle that apparently puts a ~60-year thermal oscillation into the global air temperature anomalies.
In your defense of Kartoffel’s post, you wrote: “First you said “climate of the first 40-50 years of the 20th century was unaffected by human-produced GHGs.” Now you’re backing off to “primarily natural forcings.”
Using the Myhre, 1998 [1] equation, the extra forcing due to increased CO2 (from 1900) produces an anomaly temperature of about 0.07 C by 1940. That anomaly is well within natural variation and is unobservable. To assume it was truly present is to assume what is to be demonstrated. You wouldn’t want to indulge circular thinking, would you.
In an empirical analysis, the only alternative to such circular thinking is to proceed on the basis that air temperature in the early part of the 20th century was driven by natural forcings, and unaffected by human-produced GHGs.
You also wrote, “ By the way, the inertia of the climate system impacts all forcings, not just greenhouse gases.”
Right. And during the early 20th century, the inertia of the climate system was derived from the natural forcings and feedbacks of prior centuries.
When I wrote, “An empirical analysis of this sort is a test of theory. Making changes to the empirical warming rates to conform with theory injects the expected into the known.”
Your reply: “Do you not see the fault of your argument? You’re trying to minimize the impact of early-20th-century greenhouse gases using IPCC model results. But those model results *demonstrate* exactly the consensus values of climate sensitivity that you’re attempting to dispute!”
Climate-system inertia due, for example, to the heat capacity of the oceans and the isothermal phase changes of water, will be part of any complete theory of climate. There’s no acceptance of any particular formulation of climate theory in recognizing that.
More to the point, there is no empirical reason to assign anything unusual or unnatural to the surface air temperature trend of the early 20th century. Therefore to use this time as an empirical baseline is valid.
The point of noting GCM predictions is that their in-built water vapor feedback gives a maximal estimate of the effect of increased CO2, and they predict an unobservably small thermal effect for the earlier 20th century
Therefore, the proposition that the thermal history of the early 20th century reflects natural forcings and feedbacks is both justified empirically and predicted by your GCMs.
Since the unbiased empirical view and the GCM view agree on an unperturbed early trend, then it is entirely valid to use the history of early 20th century air temperatures to test the prediction of GCMs as regards the later 20th century surface air temperatures. During this later time only, do GCMs predict a detectable anthropogenic thermal effect.
There is no “fault” to my argument. Anyone who thinks GCMs actually predict surface air temperatures, in the scientific meaning of “predict,” will have to agree that the comparative early/late test is valid.
And in the event, the test falsified the prediction.
Finally, by this statement, “I guess you’ll accept IPCC models as evidence — unless you don’t want to.” shows that you didn’t see the very standard scientific reasoning I’ve described above, about how to use data to test a theory. I’m surprised you missed it.
Theories do not produce “evidence,” by the way. Theories, falsifiable in science, produce predictions and provide explanations (meaning). Evidence in science is strictly the province of observation and experiment. Evidence tests theory, theory provides meaning and produces analytically testable predictions. Your supposition that GCMs provide evidence is to fundamentally misconstrue theory and result in science.
[1] G. Myhre, et al., (1998) “New estimates of radiative forcing due to well-mixed greenhouse gases” Geophys. Res. Lett. 25(14), 2715-2718, Table 3.
Ken, your criticisms of my article in Skeptic rested on discredit by personal attack, just as does your criticism here.
No it doesn’t – the whole Skeptic article was based on the argument – “If the uncertainty is larger than the effect, the effect itself becomes moot.” – which was presented as a truism, without being shown to be entirely, mostly or in any scientific sense, a statement of truth. It’s a rhetorical statement meant to be convincing only to those without intimate knowledge of climate modelling. Which I admit I am not, however I think I am correct that GCM’s are, as much as possible, based on real physical processes and those impose their own limits on how far that uncertainty can take real world changes. Your ‘toy’ model had no such limitations and could produce an ever widening fan of uncertainty that GCM’s would not and don’t.
As was pointed out to you at the time your modelling bore no relationship to GCM’s and revealed nothing about them. It did, however, reveal much about your own ignorance of climate modelling – which appears to be even greater than my own.
I’d like to add that I think the ‘uncertainty greater than the effect makes the effect moot’ idea, applied elsewhere – such as to the daily progression from winter to summer – shows how devoid of substance this argument is. After all, the differences day to day are highly uncertain – disconnect them from the underlying physical processes and that uncertainty would blow out and leave us thinking we can’t have any confidence in predictions that summer will be hotter than winter. Clearly the effect, despite being overwhelmed by day to day uncertainty, is not moot. A bit simplistic perhaps, yet any model that fails to base itself on the physical processes will fail to be constrained by them. I think your modelling was of that sort – which I took to be Gavin Schmidt’s point.
“As Tamino points out, a linear slope (slope plus intercept) plus a sinusoid (amplitude plus phase) comprises 4 parameters. ”
Thanks, Rick, for your brilliant summation… One small correction, though. A linear + sinsusoid fit is actually FIVE parameters: slope & intercept, plus amplitude, PERIOD and phase. All of this to fit *two* mild deviations from the linear fit: a cool period (-1.5 sigma below linear trend) around 1915, with CO2 of 300ppm, and a warm period in the 1940s, (+2 sigma above, CO2 at 310 ppm). So the situation is even more ridiculous than you suggest.
Elephants.
Rick A. Baartman wrote:
Phil Bennett wrote:
“Give me four parameters and I can fit an elephant. Give me five and I can make it wiggle its tail.”
Joel, a conservative approach is that without any evidence of a large external perturbation, the climate of the early 20th century can be taken as cooking along under its own natural impetus. One needn’t make any assumptions at all about rates of warming or cooling. That position doesn’t rig anything.
PJKar, if you think there’s something foolish about my E&E paper, please do provide a substantive criticism.
You’re right that I proceeded with the examination of the global surface air anomaly trend on the presumption that it is physically real. So, the analysis was openly stated to be an exercise with the originating assumption also stated right up front and at the beginning. How is that fraudulent?
You’re also right that Bob Tisdale didn’t like the AMO+PDO summed curve I referenced. His objection had nothing to do with whether they show ~60 year periodicity (pdf download), and, also, which was the point of the analogy I made.
I’m referring to the article at Watt’ss site.
To reiterate you first trash the climate data with this:
“It seems certain that surface air temperatures are so contaminated with systematic error – at least (+/-)0.5 C — that the global air temperature anomaly trends have no climatological meaning.”
You then go on to develop set of conclusions on climate sensitivity, warming trends and the existence of climate oscillations based on data that you admit has no climatological meaning.
So why would you expect anyone to accept your conclusions when you claim the data on which they are based has no climatological meaning. If your input data has no climatological meaning then how can your conclusions have any climatological meaning? There isn’t even a starting point for discussion when you present such a self-contradictory opening to your article because you immediately kill your own credibility.
Its laughable. I mean its hilarious Pat. And to try and pass this off as climate science is a joke. Yes fraud is an appropriate choice of words Pat. I take no pleasure in saying it but in my opinion that’s what it is.
Also I believe it would be a waste of time for anyone to engage you on a single point in your argument until you somehow resolve the contradiction which you have trapped yourself with
Pat Frank says, ” a conservative approach is that without any evidence of a large external perturbation, the climate of the early 20th century can be taken as cooking along under its own natural impetus. ..”
Uh, no. A conservative approach is one that is 1)consistent with known physics, 2)consistent with known evidence. Your approach is consistent with neither criterion, How, pray, is temperature supposed to rise unless there is a net input of energy? How are the poles and the glaciers melting, the planet drying, etc. if the temperature isn’t rising? Your analysis is not merely wrong. It is silly.
Some of my links seem to have an extra quotation mark at the end, and produce a 404 error. My apologies.
Sorry Tamino I didn’t mean to embed this video, only link to it.
[Response: And it’s kinda gross.]
If you carefully read Frank June 13, 2011 at 12:04 am , he essentially refutes himself.
I find it interesting…
Right you are–his reasoning is essentially the inverse of that which he decries as ‘circular.’ But a negative assumption no more justifies itself as a conclusion than does the corresponding positive assumption.
Sorry Phil, my bad. Note that a quartic polynomial also has 5 parameters. Anybody want to fit the 1880-to-present data to a quartic? That would be good for a laugh.
Pat Frank says:
“The zero slope of the residuals, not of the fits to the residuals, shows that all of the signal is accounted for in the cosine+linear fits. The zero slope fits to the zero slope residuals just visually emphasizes this fact. No significant excursions. This is not very hard to understand.”
I would point out that the zero slope of the residuals is a necessary result of having done a linear fit (plus sinusoidal) to the original data and does not demonstrate that the fit model accounts for “all of the signal” (QUITE a claim!).
It also does not mean that there are “no significant excursions” of the actual data from the fit model. Correct me if I’m wrong, but if the residuals were a perfect and symmetric V, you’d get a zero slope. Casual observation (and that’s all you’ll get from me at this hour) hints at the model overestimating the linear slope in the first half of the period and underestimating the slope in the latter half. This suggests that the processes driving temperature is not well represented by PF’s egregiously simple and non-physical linear+sinusoidal model.
PF,
Your mistake is in thinking curve-fitting, especially with sinusoids, can demonstrate anything physical. You can fit ANY curve with enough sine terms. There’s a whole separate field of applied math dedicated to doing just that: Fourier analysis.
What Ptolemy did with his geocentric solar system was essentially to Fourier-analyze planetary motions. That’s how he wound up “proving” that planets moved in epicycles on deferents. Don’t misunderstand me. Ptolemy was no fool. He was going on pure empirical evidence and his math was extremely good for his time–especially considering that he had to work with Greek numeric notation. But he didn’t understand statistical analysis because there was none in his time.
I made the same mistake as a teenager. I fit a sinusoidal pattern to the semimajor axes of the planets, seeking an “improved” Bode’s Law. I got lots of good fits, but they didn’t mean anything. I was writing equations with multiple transcendental functions and up to seven constants–to fit ten planets. Bad idea. The fit was impressive, but statistically meaningless.
Unless you have some a priori reason to suspect a sinusoidal effect, and have observed enough oscillations to be sure what you’re seeing is a cycle and not oscillation or, worse, random changes, “Almost two full cycles” just isn’t enough. It’s like observing the US economy during the Great Depression and the World War II boom and concluding that the US economy is cyclic. There is a “business cycle,” but it’s not what scientists mean by “cyclic.”
Let me clarify a few terms here:
A cycle is a regular motion of nonzero amplitude and wavelength. Example: The seasons.
An oscillation is irregular in both amplitude and wavelength, Examples: ENSO or the PDO. You could say a cycle is a special case of an oscillation, but that’s true only technically.
Random variation: Almost every time series there is goes up and down because most things we track have multiple causes. Examples: The economy, or which party holds the White House or Parliament.
As many have pointed out, a linear fit results in residuals that have no linear part. That’s a mathematical fact. But this does not work if we go beyond linear. The reason is that a linear fit is two terms a+bx, but the next term cx^2 does not average to zero so interferes with the constant term a. To continue fitting in such a way that adding higher order terms leaves the first ones unchanged, one must use not 1,x,x^2,x^3, etc. but a set of orthogonal polynomials. For example, using Legendre polynomials requires the quadratic term to be 3x^2-1. This would require scaling time so that the year 1880 maps to x=-1 and 2011 maps to x=1. But those chosen dates are arbitrary and such fits even if taken to sufficiently high number of terms that every single year is exactly fitted (always possible for a complete set of orthogonal polynomials but requiring as many terms as there are years) tell one absolutely nothing about the underlying physics.
[Response: I’m afraid you’re mistaken. Fit a quadratic (y = a + bt + ct^2) and the residuals will necessarily have zero linear slope.
In fact, Legendre polynomials are still polynomials, and any linear combination of Legendre polynomials of maximum order n is equivalent to a polynomial of order n. So whether you fit a straight polynomial, or an orthonormal set, you’ll end up with the same fit and the same final polynomial.
The salient point in regression isn’t the fit functions (powers of time vs. Legendre polynomials), it’s the *subspace* spanned by the fit functions. Powers of time up to degree n, and Legendre polynomials up to degree n, are not equivalent — but the subspaces they span are equivalent.]
I guess we’re crossed up here because I explained it clumsily, using the quadratic/constant example instead of one that impacts the linear term. The constant term will certainly change if you add an x^2 term to the fit, since the average of x^2 is not zero. In the same way, the linear term will change if you add a cubic term. And so on. This is at least true of the way I do fits. Perhaps you do them differently.
[Response: Yes if you add a quadratic/cubic term the constant/linear coefficients will change. But the residuals will still have zero mean and zero slope.
If you do a linear fit, then all purely linear functions lie in the subspace of model functions, so the residuals have zero linear slope. If you do a quadratic or cubic (or higher order polynomial) fit, then all purely linear functions still lie in the (now higher-dimensional) subspace of model functions, so the residuals still have zero linear slope. The particular linear term which best matches your data may be different, but your residuals will still be orthogonal to all purely linear functions.
And those subspaces are the same whether your model functions are powers of time, or Legendre polynomials.]
I’m a humble geophysicist. Therefore I won’t say that much about curve fitting.
however, in “geophysicist” there is “physicist”, and as a pavlovian reflex I searched for the brilliant explanations of Mr Frank about the physic guiding him in his quite long answer.
I found these explanations :
“Atmospheric CO2, by the way, traps energy not heat. How the climate works determines whether that energy appears as sensible heat. Your analysis is careless.”
and
“You’ve made yet another untoward inference. My analysis was an exercise in physical phenomenology. That’s when one takes real physical data (temperature anomalies) and, within a physical context (global thermal behavior), uses physical reasoning to examine the data in terms of mathematical functions that reflect common natural phenomena (cycles).”
Now I know. Thanks, Mr Frank.
By the way, was there something I missed, because after the second quote I stopped reading …
One of the problems here is how we establish the difference between cyclic behaviour and non cyclic behaviour. Let’s take a little example. Here’s the hadcrut3v data from 1975 to 2000 with a 60 month smooth and the linear trend roughly removed.
http://www.woodfortrees.org/plot/hadcrut3vgl/from:1975/to:2000/mean:60/detrend:0.28
There’s a very clear 8 year cycle. It stands out like a sore thumb. What does this tell us?
Well, nothing. If we compare it with the forcing data, then we immediately see that there are two troughs caused by volcanoes. Fitting a linear+cosine function gives a good fit, but tells us nothing about what is going on – indeed it misleads us into thinking we’ve found a cycle when there isn’t one. If we go beyond the fitting period, then we’ll immediately see our error. That’s the first reason why Tamino tried omitting the last 10 years from the fit.
The second problem is more complex. You need to know a bit of Fourier theory, and in particular the convolution theorem: http://en.wikipedia.org/wiki/Convolution_theorem
Our data is limited to a certain time frame. We can only fit the cosine wave within this frame. The limited time frame is equivalent to multiplying an infinite time series by a box function covering the time frame – 130 years in our case.
When looking for cycles, we are looking for peaks in the Fourier spectrum (the frequency domain in the case of a time series). But multiplying a time series by some function has the same effect as convoluting the frequency spectrum with the Fourier transform of that function. This smears out the peaks of the Fourier spectrum. In the case where the box function is only one or two cycles, the peaks in the spectrum become so spread as to interefere with eachother, and also for the location of the maximum to be poorly determined. That’s the second thing we see when Tamino cut out 10 years of data. The length of the cycle changed because you can’t realistically identify cyclic behaviour from only 2 repeats.
[edit]
[Response: Enough already.]
Dear Tamino,
could we at least know the general topic of his answer ? More meaningless maths, or more absurd physic ?
I’d guess it was a rehash of what he’s already blessed us with.
Just be thankful you can take your boots off.